Теплообмен излучением между поверхностями, разделенными ослабляющей средой

Излучение в ослабляющей среде

В металлургической практике широко распространены такие случаи теплообмена излучением, когда излучающие поверхности разделены ослабляющей средой. Ослабляю­щей средой могут являться газы, излучающие и поглоща­ющие тепловую энергию, а также газы с взвешенными в них частичками сажистого углерода и золы. В объемах, заполненных такой средой, проходящий лучистый поток будет ослабляться, так как частицы среды способны погло­щать и рассеивать тепловую энергию. Наиболее часто встречаются такие случаи (газы, газы со взвешенными от­носительно мелкими частицами), для которых ослабление излучения происходит за счет поглощения, а рассеяние от­сутствует вовсе или им можно пренебречь.

Закон Бугера — Вера. Согласно закону Бугера, относи­тельное ослабление луча в слое среды пропорционально толщине этого слоя dх. Однако, согласно закону Бера, от­носительное изменение интенсивности луча в слое данной толщины пропорционально концентрации ослабляющего вещества m. Отсюда следует объединенный закон Бугера — Бера

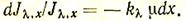(57)

Коэффициент пропорциональности k_lхарактеризует способность частиц поглощать и рассеивать излучение волн длиной lи называется спектральным коэффициентом ос­лабления.

Интегрированием выражения (57) можно найти интен­сивность луча, прошедшего через слой толщиной S. Если k_l и m не зависят от х, то

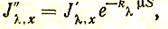(58)

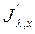где и 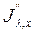— интенсивность излучения в начале и конце слоя толщиной S.

Так как газовые среды практически не отражают пада­ющее на них излучение (R = 0), то, согласно определению, поглощательная способность равна отношению поглощен­ного потока к падающему:

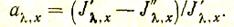(59)

Из выражений (58) и (59) следует, что для ослабляю­щей среды

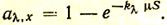(60)

Согласно закону Кирхгофа, для равновесной системы спектральные степень черноты и поглощательная способ­ность равны. Поэтому можно записать

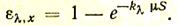(61)

Из формул (60) и (61) следует, что а_l,х и e_l,х тем боль­ше, чем больше произведение mS.

Поскольку одни и те же частицы реагируют на излуче­ние волн разных длин неодинаково, то закон Бугера — Бера не всегда справедлив для интегрального излучения. Ос­лабление последнего происходит преимущественно в ре­зультате ослабления отдельных волн; другие волны могут вообще не ослабляться.

Закон Бугера—Бера достаточно точно соблюдается лишь при малых концентрациях поглощающего вещества, когда взаимодействие между частицами практически отсут­ствует. При больших концентрациях k_l зависит от m, а следовательно, степень черноты и поглощательная способность слоя зависят не только от mS, но и от m.

Для упрощения практических расчетов обычно вводят понятие серый газ, т. е. такой газ, поглощательная способ­ность (следовательно, и e) которого во всех частях спектра одинакова.

Излучение газов

Спектр поглощения газов является селективным. Это означает, что газы поглощают тепловую энергию в опреде­ленных интервалах длин волн Dl, определяющих так на­зываемые полосы поглощения. Как следует из закона Кирх­гофа, газы могут испускать лучи только с теми длинами волн, что и лучи, которые они поглощают. Поэтому излуче­ние газов является также селективным. Не все газы прак­тически излучают и поглощают тепловые лучи. Спектр встречающихся в составе печной атмосферы одно- и двух­атомных газов (кислорода, азота, окиси углерода и др.) состоит из очень узких полосок, поэтому общее количество энергии, которое излучают эти газы, очень невелико, и прак­тически можно считать, что они совсем не излучают тепла. Вместе с тем эти газы являются также лучепрозрачными и практически не нагреваются при прохождении через них лучей от других тел.

Трехатомные и многоатомные газы, наоборот, могут из­лучать и поглощать большое количество тепла. Наиболь­шее практическое значение имеет излучение углекислоты (СО₂) и водяных паров (Н₂О), поскольку из них (наряду с азотом) в основном состоят дымовые газы. Спектры этих газов очень сложны. Для СО₂ обычно принимают три по­лосы излучения и поглощения, соответствующие следую­щим интервалам длин волн, мкм: 2,3 — 3,02; 4,01 — 4,80 и 12,5—16,5.

Для Н₂О эти интервалы длин волн соответственно рав­ны 2,24—3,27; 4,8—8,5 и 12,0—25,0 мкм.

Поглощение газами тепловой энергии зависит от тем­пературы и концентрации газа, выражаемой его парциаль­ным давлением и эффективной толщиной газового слоя, т. е.

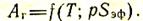
Сохраняя единообразие записи с твердыми телами, мож­но написать то же самое для степени черноты газов:

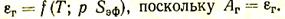
Излучение газами тепловой энергии, как показали ис­следования, для СО₂ пропорционально T^3,5, а для Н₂О про­порционально T³. Применение различных законов излуче­ния для твердых и газообразных тел очень сильно затруд­нило бы расчет. Поэтому для практических расчетов теплового излучения газов применяют также закон Стефа­на — Больцмана, причем степень черноты газа также ха­рактеризует его излучательную способность. Таким обра­зом, количество тепла, которое излучает газ на 1 м² окру­жающей его поверхности, в единицу времени может быть найдено из выражения

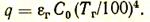
Погрешность, вносимая допущением о том, что q_г = f(T⁴), учитывается при определении e_г.

Определение степени черноты газов. Как указывалось выше, степень черноты газов зависит от температуры газа, его парциального давления и средней длины пути луча. Обычно температура газов известна. Парциальное давле­ние газов можно получить из расчета горения топлива. Так, если в продуктах сгорания содержится 10% СО₂ и 15°/о Н₂O, то, следовательно, их парциальные давления соответственно равны 0,1 и 0,15 общего давления печной среды, которое равно практически давлению атмосферы.

Среднюю длину луча можно определить по формуле

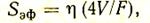(62)

где V — объем, заполненный излучающим газом, м³; F — поверхность всех стенок, ограничивающих этот объем, м²; h — коэффициент, обычно принимаемый равным 0,9.

Для определения степени черноты газов пользуются графиками, приведенными на рис. 34—36, с помощью кото­рых находят степень черноты 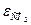и условную степень черноты водяных паров 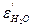. Степень черноты водяных паров необходимо умножить на поправку, которую находят по рис. 36, и в результате .

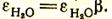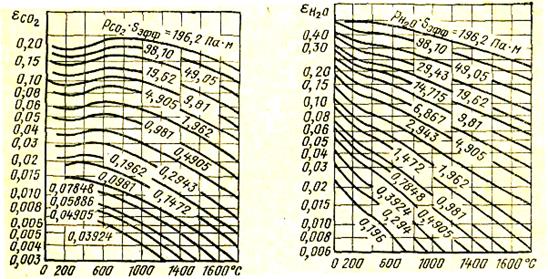
Рис. 34. Номограмма для определе- Рис. 35. Номограмма для определе-

ния степени черноты СО₂ ния степени черноты Н;О

Степень черноты газов находят суммированием получен­ных степеней черноты отдельных газов:

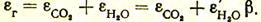
Теплообмен излучением между излучающим газом и стенками. Нагретый газ излучает на 1 м² поверхности ок­ружающих его стенок количество тепла, определяемое по выражению

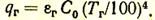
С единицы поверхности стенок излучается тепловой по­ток с плотностью

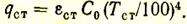
Газ и стенки поглощают только часть лучей в соответ­ствии с их степенями черноты. Часть лучей газами будет пропущена и попадает снова на стены, которые определенную долю поглотят, а остальное снова отразят и т. д. Проанализировав весь ход этих многократных поглощений, от­ражений и пропусканий лучистых потоков, Г.Л. Поляк на­шел следующую формулу для расчета теплового потока, передаваемого излучением от газов к стенкам (или от сте­нок к газу, если Т_г<Т_ст):

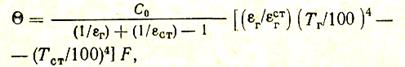(63)

где e_г — степень черноты газа при Т_г,К; 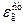— то же, газа при T_ст, К; e_ст — то же, стенки при T_ст, К.

Теплообмен в замкнутой си­стеме из двух поверхностей, разделенных ослабляющей сре­дой (серый газ). Рассмотрим случай теплообмена двух серых поверхностей (см. рис. 31, б), образующих замкнутый объ­ем, заполненный серым газом. Допустим, что поверхность F₂адиабатная. Это означает, что эффективное излучение этой поверхности равно падающе­му на нее лучистому потоку. Поверхность F₁по выбранной схеме представляет собой тепловоспринимающую поверхность (поверхность нагреваемого материала). Поэтому целью данного вывода является определение результирую­щего потока поверхности F₁.

Падающий на поверхность F₁поток равен излучению газа 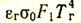плюс эффективное излучение поверхности F₂,попадающее на поверхность F₁и ослабленное при прохож­дении через газ,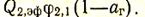

Результирующий поток равен разности между падаю­щим потоком и эффективным излучением. Таким образом, результирующий поток поверхности F₁

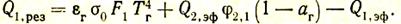(64)

Эффективное излучение поверхности F₁можно найти по формуле (53):

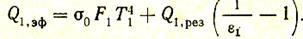
Для нахождения Q_2,эф воспользуемся тем, что поверх­ность F₂ адиабатная и ее эффективное излучение равно па­дающему потоку. Последний складывается из излучения газа на поверхность F₂,эффективного излучения поверхно­сти F₁,ослабленного газом, и части (j_2,2 = 1 — j_2,1) эффек­тивного потока, излучаемого поверхностью F₂самой на себя, также ослабленного при прохождении через газ. Та­ким образом,

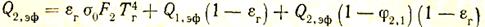
или

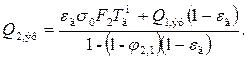
Подставляя значения Q_2,эф и Q_1,эф в уравнение (64) и учитывая, что для серого газа а_г = e_г,после необходимых алгебраических преобразований получаем

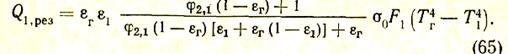
Выражение (65) называют формулой Тимофеева В.Н. и широко применяют для расчета теплообмена в промыш­ленных печах и топках котлов.