Элементы теории движения реальных газов
При движении газа на каждый его объем будут действовать не только те силы, которые характерны для статики, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеального газа этими дополнительными силами будут силы инерции, а для реального газа — силы инерции и трения (вязкости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих математических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье — Стокса). Уравнения Навье — Стокса настолько сложны, что к настоящему времени решены лишь для крайне ограниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Таким образом, получено одно из важнейших уравнений гидро- и аэродинамики — уравнение (закон) Бернулли.
Уравнение Бернулли. В практических условиях крайне распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизменным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).
Для несжимаемого газа (r = const) уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид
rgz +р +rw2/2 = const. (14)
В соответствии сэтим величина р является статическим давлением, величина rgz — геометрическим давлением, величина rw2/2 — динамическим давлением.
Уравнение Бернулли представляет собой закон сохранения энергии, поскольку сумма р + rgz характеризует потенциальную, а величина rw2/2 — кинетическую энергию.
Как отмечалось выше, в металлургической теплотехнике в подавляющем большинстве случаев пользуются давлением, избыточным над атмосферным. Поэтому полезно уравнение Бернулли привести к такому виду, при котором все члены его были бы выражены в избыточных давлениях. Для этого представим себе канал, окруженный воздухом плотностью rв, по которому движется газ плотностью rг. Принимая плотности газа и воздуха неизменными, напишем уравнение Бернулли и для газа и воздуха применительно к сечениям канала z1и z2.
Уравнение для газа
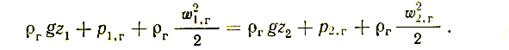
Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)
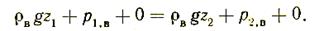
Вычитая из первого второе, получаем уравнение Бернулли для газа в избыточных давлениях:
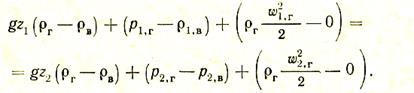
(15)
Если перейти к ранее принятому обозначению через h, то уравнение можно соответственно переписать в таком виде:
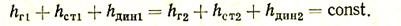 (15¢)
(15¢)
Однако равенство hS1 = hS2 строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Но если по каналу перемещается реальная (вязкая) жидкость (газ), то часть энергии тратится на преодоление различных сопротивлений и происходит потеря энергии.
В этом случае при движении от сечения I к сечению II
hS1 = hS2 + hпотерь (16)
и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жидкости (газа) для различных сечений канала сумма давлений всех видов является постоянной».
Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли.
При движении реального газа часть его энергии расходуется на преодоление различных сопротивлений.
Различают потери на трение и потери на преодоление местных сопротивлений. Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при повороте канала или усложнении его сечения (трубчатый пучок). Величину потерь напора выражают в долях динамического давления.
Потери на трение Лтр можно определить по формуле (Па)
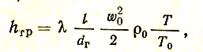 (17)
(17)
где l — коэффициент трения; l — длина канала, м; dг— гидравлический диаметр канала, м (для некруглого сечения канала dг =4F/П, F — площадь сечения канала, м2; П — периметр канала, м); r0 и w0 — плотность и скорость жидкости (газа) при нормальных условиях, т. е. при атмосферном давлении и температуре Т0, равной 273 К; Т — действительная температура жидкости или газа, К.
При ламинарном движении (Rе < 2300) коэффициент трения зависит от критерия Rе
l = 64/Rе. (18)
При турбулентном движении коэффициент трения зависит не только от критерия Rе, но и от относительной шероховатости стенки канала (D/d), равной отношению абсолютной шероховатости D (в мм) к диаметру канала d:
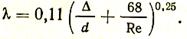 (18¢)
(18¢)
При приближенных практических расчетах коэффициент трения l можно принимать постоянным и равным для кирпичных каналов 0,05, для металлических 0,04.
Потери на преодоление местных сопротивлений определяются по формуле (Па)
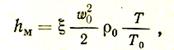
где x— коэффициент местных сопротивлений. Его величина зависит от формы местного сопротивления и, как правило, определяется опытным путем.
Важнейшим расчетом, который выполняется для подавляющего большинства печей, является определение суммарных потерь давления на пути движения дымовых газов от печи до дымовой трубы. Суммарные потери используются при определении размеров дымовой трубы, которая рассчитывается из условия, что разрешение, создаваемое дымовой трубой, должно быть по абсолютной величине больше суммы всех сопротивлений, возникающих в дымовом тракте печи (см. том 2-й настоящего издания).
Таким образом, уравнение (закон) Бернулли находит очень широкое применение. Наряду с уравнением Бернулли важную роль в гидро- и аэродинамике играют также уравнение сплошности и уравнение импульсов Эйлера.
Уравнение сплошности. В практических условиях наиболее распространенными являются такие процессы, при которых масса газа, протекающая по какому-то объему, остается неизменной. При этом, естественно, масса газа, втекающая в объем в единицу времени, должна быть равна массе вытекающего газа.
Следовательно, можно написать, что т1 = т2, или, учитывая, что масса есть произведение скорости, сечения потока и плотности, получаем
w1f1r1 = w2f2r2.
При условии постоянства плотности (r1 = r2) последнее выражение принимает вид
w1f1 = w2f2. (19)
Если в качестве скорости принимать среднюю скорость потока, то выражение (19) применимо для практических расчетов при течении в трубах и каналах, причем средняя скорость потока определяется как частное от деления секундного объема среды, проходящего через данное сечение, на величину площади сечения, т. е.
w = V/f.
Уравнение импульсов Эйлера. Уравнение импульсов (количеств движения) Эйлера имеет важное значение для некоторых практических расчетов. Это уравнение применимо к какому-то воображаемому контуру, выделенному в общем потоке газа, через боковую поверхность которого ни движения, ни массообмена не происходит.
В подобном контуре под действием внешних сил (в потоке газа под действием давления) происходит изменение количества движения газа. Если изменение импульсов проходящего газа и изменение внешних сил отнести к единице времени, то теорема импульсов Эйлера может быть сформулирована следующим образом: «Изменение импульса всех сил, приложенных к газу, проходящему через выделенный контур, равно результирующей внешних сил, действующих на данный контур».
Записывается это уравнение так:
SD(mw) = SP. (20)
Применение уравнения импульсов будет проиллюстрировано ниже при рассмотрении струйных аппаратов. Расчеты инжекторов и эжекторов с использованием выражений, полученных на основании применения уравнения импульсов Эйлера, приведены во 2-м томе настоящего издания.
Дата добавления: 2015-11-10; просмотров: 1657;
