Применение уравнения Бернулли

Трудно назвать раздел механики газов, где не исполь­зовалось бы в той или иной мере уравнение Бернулли. По­знакомимся лишь с некоторыми наиболее важными случа­ями применения этого уравнения.

Истечение газов через отверстия и насадки

Истечение газов через отверстия и насадки наблюдает­ся при работе горелок, форсунок, при выбивании газа через отверстия в стенах печи и в других случаях. Установим связь между количеством вытекающего газа и размерами отверстия и давлением, под которым происходит истече­ние. Для простоты возьмем истечение несжимаемого газа, температура которого в процессе истечения практически не изменяется.

Отверстия с острыми краями. Положим, что из сосуда очень больших размеров, давление в котором р₁, газ выте­кает через отверстие сечением f₀ в среду с давлением р₂. Для определения скорости истечения газа w₂ напишем уравнение Бернулли для сечений I и II (рис. 9). Поскольку температура газа неизменна, постольку h_г1 = h_г2. В этом случае, пренебрегая потерями, можно написать

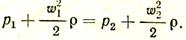(21)

Вследствие большого размера сосуда можно принять w₁= 0

Тогда

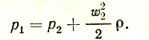
Отсюда

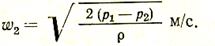(22)

В силу инерции частичек истекающего газа сечение струи f меньше сечения отверстия f₀. Отношение f/f₀= e называется коэффициентом сжатия струи. Скорость w₂ фактически относится не ко всему сечению отверстия f₀, а лишь к сечению струи f. Для определения расхода газа че­рез отверстие f₀ найдем V = w₂f. Но f = ef₀ следовательно,

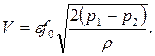(23)

С учетом гидродинамических потерь при истечении че­рез отверстие выражение (23) принимает вид (м³/с)

(24)

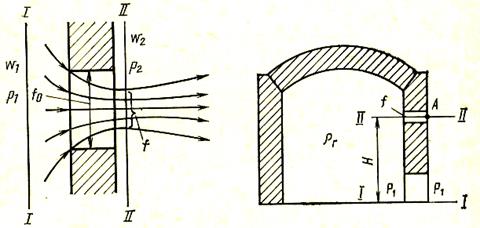
Рис. 9. Истечение газа из отвер- Рис. 10. Истечение из отверстия в

стия в тонкой стенке стечке печи

Смысл коэффициентов j и m, ясен из следующего при­мера.

Истечение из отверстия в стенке печи (рис. 10) — весь­ма распространенный на практике случай. Рассмотрим подобный случай истечения (с учетом потерь) из отверстия сечением f, расположенного на высоте Н от уровня пода печи. Напишем уравнение Бернулли для сечения I и точки А в сечении II:

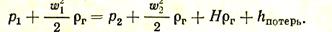
Скорость движения газов в отверстии w₂много больше скорости w₁; исходя из w₂ññ w₁, принимаем w₁ = 0.

Как следует из изложенного выше, потери на местные сопротивления могут быть определены как

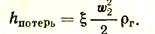
Так как печь сообщается с атмосферой на уровне пода, то статическое давление газа внутри печи и давление воз­духа снаружи равны между собой и равны р₁.

Давление р₂ в точке А соответствует атмосферному дав­лению на высоте H от уровня сечения I, т. е.

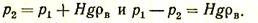
С использованием этих зависимостей уравнение Бернул­ли принимает вид

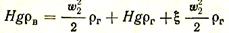
или

Отсюда

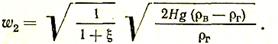(25)

Величина 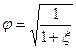учитывает гидравлическое сопро­тивление отверстия, через которое происходит истечение.

Количество истекающей из рассматриваемого отвер­стия среды (м³/с) V = w₂f₂, где f₂ — сечение струи, м².

Но если использовать понятие коэффициента сжатия струи e = f₂/f, то

.

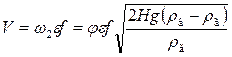Произведение je = m называют коэффициентом расхода.

Истечение через насадки. Насадком называют короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадка обычно составляет 3—4 его диаметра. Ко­личество газа, протекающее через насадок, при прочих равных условиях зависит от формы входных кромок и формы самого насадка. Рассмотрим насадки трех видов, представленные на рис. 11. Пользуясь уравнением (22), получим для них следующие расчетные формулы: для насадки с открытыми кромками

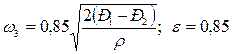(26)

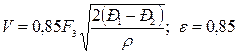(27)

Для насадков с закругленными кромками и диффузора

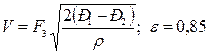(28)

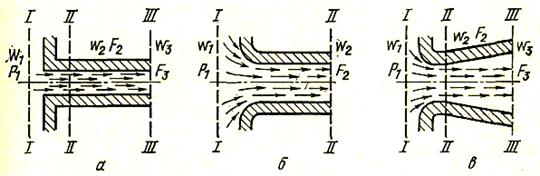
Рис. 11. Истечение газа через цилиндрические насадки:

а — с открытыми кромками; б — с закругленными краями; в — диффузор

Для этих насадков в сечении ІІІ сечения струи и отвер­стия равны друг другу и поэтому здесь e = 1,0. Сравнение выражений (26), (27) и (28) показывает, что наибольший расход при одинаковом значении р₁ — р₂и при одинаковом минимальном сечении насадков получается при истечении газа через диффузор, так как площадь выходного сечения у диффузора F₃больше, чем у насадков других типов. Угол конусности диффузора не должен превышать 6—7° во избежание отрыва потока от стенок диффузора.

Истечение газов через небольшие отверстия в стенках печи (например, гляделки) можно рассчитывать по фор­мулам для цилиндрического насадка.

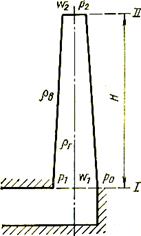Дымовая труба. Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разрежение соз­дается в дымовой трубе благодаря стремлению горячих газов подняться, обусловленному, как будет показано ниже, разностью плотностей холодного наружного воздуха и горячих газов. Найдем зависимость разреже­ния, создаваемого трубой, от высо­ты трубы Н и температуры газов. На рис. 12 представлена схема ды­мовой трубы. За уровень отсчета принимаем сечение ІІ. Напишем уравнение Бернулли в избыточных давлениях для сечений І и ІІ:

h_г1 + h_ст1 + h_д1 = h_ст2 + h_д2 + h_пот.

Труба в сечении II сообщается с атмосферой, поэтому h_ст2 = 0. Из приведенного выше уравнения сле­дует, что статическое давление в основании трубы

h_ст1 = – h_г1 + h_д2 – h_д1 + h_пот.

Ввиду незначительных скоростей движения газов в тру­бе величины потерь, выражаемые в правой части приведен­ного выше уравнения тремя последними членами, значи­тельно меньше абсолютной величины потери, выражаемой первым членом. Следовательно, статическое давление в основании трубы будет отрицательным, т. е. там будет разрежение. Умножив правую и левую части последнего уравнения на минус единицу, получаем

– h_ст1 = h_раз = h_г – (h_д2 – h_д1) – h_пот. (29)

Потери давления в трубе h_пот складываются из потерь на трение h_тр и потерь, возникающих при выходе газов из трубы в атмосферу и равных xh_д2. Учитывая, что коэффи­циент местного сопротивления на выходе из трубы ра­вен единице (x = 1), можно написать, что

h_пот = h_тр + h_д2.

Вследствие этого уравнению (29) можно придать сле­дующий вид:

h_раз = h_г + h_д1 – 2 h_д2 – h_тр. (29¢)

Для того чтобы получить окончательное выражение для h_разр, в уравнение (29) необходимо подставить все входя­щие в него величины. Температура газов по высоте дымо­вой трубы и ее сечение существенно изменяются, поэтому принимаемые в расчете плотность и скорость движения га­зов в дымовой трубе определяются по средней температу­ре по высоте трубы. Величина геометрического давления h_г, входящего в уравнение (29), выражается уравнением (13). Динамические давления будут соответственно равны

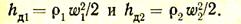
Потери давления на трение находят по уравнению

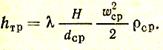
Подставив в уравнение (29') значения h_г, h_д1, h_д2, h_тр и выразив их через скорости и плотности при нормальных условиях (w₀ и r₀) по указанным выше выражениям, окон­чательно получаем (Па)

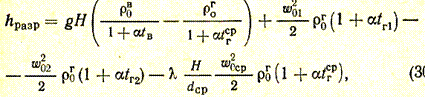(30)

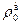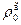где h_разр — действительное разрежение в основании дымо­вой трубы (сечение I), Па; и — плотность соответст­венно воздуха и газов при нормальных условиях, кг/м³; d_ср — средний по высоте диаметр трубы, м; w₀₁ и w₀₂ — скорость газов в сечениях I (в основании трубы) и II (в устье трубы) при 0°С, м/с; w_0ср — средняя скорость га­зов по высоте трубы при 0°С, м/с; t_в — температура окружающего воздуха, °С; 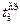— средняя температура газов по высоте трубы, °С; t_г1 и t_г2 — температура газов в сечениях I и II, °С.

Если учесть, что

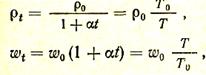
где Т₀ = 273 К,то выражение (30) может быть переписано следующим образом:

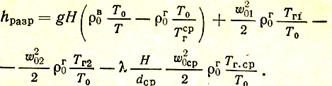
Отсюда

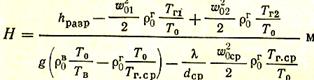(30¢)

В расчетах разрежение в основании дымовой трубы принимают обычно с запасом, равным h_разр = 1,3S h_пот. Ве­личина S h_пот представляет собой суммарные потери напо­ра на пути движения газов от печи до основания дымовой трубы.

При расчете дымовой трубы внутренний диаметр в устье ее d_у(на выходе) принимают, исходя из скорости газов, равной 3—10 м/с (при скорости выхода газов, не меньшей 3 м/с, при ветре может происходить их задувание в трубу). Кирпичные и железобетонные дымовые трубы для большей устойчивости делают более широкими в основании. При расчетах внутренний диаметр в основании трубы d₀прини­мают в 1,5 раза больше внутреннего диаметра устья трубы d_у, т. е. d₀= 1,5d_у.

По условиям выполнения кладки d_удля кирпичных труб не должен быть меньше 0,8 м.

Падение температуры газов на 1 м высоты трубы при­нимается для кирпичных и железобетонных 1,0—1,5 °С, а для металлических 3—4°С. Ориентировочно высота тру­бы может быть определена по уравнению (30) без трех последних его членов.

Подсчитав сумму потерь всех видов на пути движения газов от печи до основания дымовой трубы, по уравнению (30') находят расчетную высоту трубы Н. Независимо от расчета высота дымовой трубы по правилам сантехники должна быть не менее 16 м и в 2 раза выше самого высо­кого здания, находящегося в радиусе 100 м вокруг трубы.