Как формулируются аксиомы метрологии?

Первая аксиома метрологии: без априорной информации измерение невозможно. Первая аксиома метрологии относится к ситуации перед измерением и говорит о том, что если об интересующем нас свойстве мы ничего не знаем, то ничего и не узнаем. С другой стороны, если о нем известно все, то измерение не нужно. Таким образом, измерение обусловлено дефицитом количественной информации о том или ином свойстве объекта или явления и направлено на его уменьшение.

Наличие априорной информации о любом размере выражается в том, что его значение не может быть равновероятным в пределах от -¥ до +¥. Это означало бы, что априорная энтропия

,

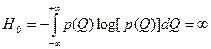и для получения измерительной информации

I = Но – Н

при любой апостериорной энтропии Н потребовалось бы бесконечно большое количество энергии.

Вторая аксиома метрологии: измерение есть ни что иное как сравнение. Вторая аксиома метрологии относится к процедуре измерения и говорит о том, что нет иного экспериментального способа получения информации о каких бы то ни было размерах, кроме как путем сравнения их между собой. Народная мудрость, говорящая о том, что «все познается в сравнении», перекликается здесь с трактовкой измерения Л. Эйлером, данной свыше 200 лет тому назад: «Невозможно определить или измерить одну величину иначе как, приняв в качестве известной другую величину этого же рода и указав соотношение, в котором она находится с ней».

Третья аксиома метрологии: результат измерения без округления является случайным. Третья аксиома метрологии относится к ситуации после измерения и отражает тот факт, что на результат реальной измерительной процедуры всегда оказывает влияние множество разнообразных, в том числе случайных факторов, точный учет которых в принципе невозможен, а окончательный итог непредсказуем. Вследствие этого, как показывает практика, при повторных измерениях одного и того же постоянного размера, либо при одновременном измерении его разными лицами, разными методами и средствами получаются неодинаковые результаты, если только не производить их округления (огрубления). Это отдельные значения случайного по своей природе результата измерения.