Коректність постановок крайових задач

Вище відзначалося, що постановка крайових задач теплопровідності містить деякі (крайові) функції, що входять у початкові і граничні умови задачі. Очевидно, що рішення задачі також залежить від цих функцій, тому що розподіл температури в тілі в кінцевому рахунку визначається його початковою температурою, тепловим станом граничної поверхні тіла (граничні функції) і наявністю в тілі теплових джерел (чи джерел). Крайові функції задачі звичайно визначаються з досвіду і тому не можуть бути знайдені абсолютно точно. Завжди неминуча деяка погрішність у визначенні початкових чи граничних умов. Ця погрішність буде позначатися і на рішенні задачі, а тому що крайова задача описує реальний фізичний процес, то рішення цієї задачі повинне характеризуватися функціями, що безупинно залежать від крайових функцій задачі. Якби не було цієї безупинної залежності, то два істотно різних процеси теплопровідності могли б відповідати практично однаковим системам крайових функцій задачі (розходження яких лежить у межах точності вимірів), тобто рішення задачі істотно залежало б від погрішностей виміру. У цьому випадку процес теплопровідності (як, утім, і будь-який інший процес, описуваний відповідними крайовими задачами) не можна було б вважати фізично визначеним такими вихідними даними задачі.

Рішення тієї чи іншої крайової задачі для якого-небудь диференціального рівняння чи системи рівнянь є стійким (щодо крайових функцій задачі) чи безперервно залежить від крайових умов, якщо яким би не було позитивним число e, знайдеться позитивне число d, коли при зміні крайових функцій задачі на величину, що не перевершує за абсолютним значенням числа d, рішення одержує в кожній точці розглянутої області і її границі збільшення, по абсолютній величині не переважаюче e. У цьому випадку відповідний процес називається фізично визначеним.

Крайова задача для якого-небудь рівняння чи системи рівнянь у розглянутій області поставлена коректно, якщо рішення цієї крайової задачі в зазначеній області існує, єдино і є стійким.

Приведемо приклад некоректної постановки задачі. Як показав Адамар, задача Коші для рівняння Лапласа 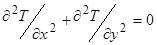в області êхê<¥, 0<y<1, при умовах Т(х,0) = 1; 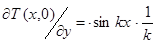поставлена некоректно. Дійсно, рішення цієї задачі є T(x,y) = (1/k²)×sh ky×sinkx. При k®0 крайова функція (1/k)×sinkx®0 рівномірна відносно х; однак рішення задачі в зазначеній області при х ¹ mp (m = 0,±1,±2…) не прагне до нуля, тобто (1/k²)sh ky×sinkx ¹ 0 при x¹mp і k ® ¥.

Якщо поставлена крайова задача теплопровідності має кілька рішень, то слова “рішення задачі” втрачають зміст. Тому перш ніж говорити про рішення задачі, необхідно довести його єдність. У фундаментальних роботах А.Н.Тихонова., А.В.Ликова та ін. показано, що рішення кожної з поставлених крайових задач єдино. При цьому для практики найбільш істотним є питання 2, тому що знаходження рішення тим чи іншим аналітичним методом фізично означає доказ існування рішення.