Винтовые оси симметрии
Винтовая ось симметрии - линия, при вращении вокруг которой на определенный угол и последующей (или предшествующей повороту) трансляции вдоль этой линии на определенное расстояние фигура совмещается с себе равной, а при повороте на 360° - со своим исходным положением в пространстве (совмещается сама с собой).
Наименьший угол, при повороте на который и последующей (или предшествующей повороту) трансляции фигура совмещается сама с собой, называется элементарным углом поворота ( 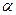 ); элементарный угол может быть равен 360, 180, 120, 90 и 60°.
); элементарный угол может быть равен 360, 180, 120, 90 и 60°.
Величина трансляции, соответствующая элементарному углу поворота, называется ходом, шагом, компонентой скольжения или элементарной трансляцией винтовой оси.
Число совмещений фигуры при повороте ее вокруг винтовой оси на 360° называется порядком винтовой оси (n). Винтовые оси, как поворотные и инверсионные оси симметрии, могут быть первого, второго, третьего, четвертого и шестого порядка.
Различают правые и левые винтовые оси. Винтовая ось называется правой, если поворот (по направлению - трансляции) происходит по движению часовой стрелки, и левой, если - против часовой стрелки.
Винтовая ось обозначается двумя цифрами (например 61). Первая большая цифра (6) указывает порядок оси. Частное от деления маленькой цифры (1) на большую (6) впереди стоящую (1/6) дает величину переноса (трансляции) вдоль оси по отношений к элементарной трансляции структуры в направлении, параллельном данной оси. На (рис. 6.3) изображены тройные оси: простая поворотная (L3) и две винтовые – правая 31 и левая 32.
Действие правой тройной винтовой оси состоит в повороте точек на 120° по часовой стрелке с последующим поступанием их вдоль оси на одну треть элементарной трансляции. В случае левой винтовой оси поворот на 120 производится против часовой стрелки.


а) простая б) винтовые правые в) винтовые левые
Рис. 6.3. Оси симметрии в призме.
6.5. Плоскость скользящего отражения
Плоскостью скользящего отражения называется совокупность совместно действующих плоскости симметрии и параллельной ей трансляции, т.е. это такая плоскость, в которой при отражении и последующей (или предшествующей отражению) трансляция параллельно этой плоскости на определенное расстояние отражённый геометрический образ совмещается с равным себе. Плоскости скользящего отражения, содержащие трансляцию, невозможны в конечных телах, они свойственны лишь бесконечным фигурам. Действие плоскости скользящего отражения показано на (рис. 6.4)


Рис. 6.4. Примеры плоскостей скользящего отражения (типа “C”)
Действие плоскости скользящего отражения можно рассмотреть на примере узора шахматной доски (рис.6.5).
Представив себе узор бесконечно протяженным, легко увидеть, что вдоль отмеченной на рисунке линии а-а проходит плоскость скользящего отражения типа "А". Действительно, чтобы совместить белый квадрат 1 с аналогичным квадратом 2, нужно первый квадрат перенести параллельно самому себе на место нижележащего черного квадрата и затем отразить в плоскости, перпендикулярной рисунку и проходящей вдоль а-а. При этом совместится весь бесконечно протяженный узор шахматной доски. Такая же плоскость будет проходить и вдоль линии а1-а1.
Вдоль линии m-m проходят обычные плоскости симметрии: шахматный узор совмещается сам с собой весь целиком при отражении в плоскости в плоскости mm без дополнительной трансляции.
Плоскости скользящего отражения изображают пунктирными или штриховыми линиями и обозначают символами А,В,С, соответственно, когда скольжение направлено вдоль осей x , y , z и величина его составляет а/2 вдоль оси x ( плоскость скользящего отражения "А"), в/2 вдоль оси у (плоскость скользящего отражения "В"); с/2 вдоль оси z. (плоскость скользящего отражения "С"). Существует еще два типа плоскостей скользящего отражения n и d
Плоскости типа " n " можно обнаружить в о.ц.к. решетке. Проекция ячейки о.ц.к. показана на рис.6.6.
Если ионы по вершинам ячейки находятся в плоскости чертежа, то ион в центре ячейки — над плоскостью чертежа на расстоянии с/2, то есть на 1/2 вдоль оси z. Это обозначено на чертеже значком 1/2. Атом из вершины ячейки может совместиться с атомом в центре, если произойдет отражение в плоскости n (нормальной к плоскости чертежа) и скольжение в этой плоскости на величину
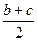 или
или 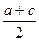
Итак, плоскость "n" - это плоскость скользящего отражения, у которой компонента скольжения направлена по диагонали параллелограмма, построенного на элементарных странсляциях, лежащих в этой плоскости, и равна 1/2 длины этой диагонали:
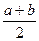 ;
; 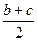 ;
; 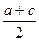

| Рис. 6.5. Плоскости симметрии m и плоскости скользящего отражения (А и В) | Рис. 6.6. Плоскости скользящего отражения типа “n” в о.ц.к. ячейке |
Плоскости типа "d", или "алмазные", возможны только в гранецентрированных решетках. На примере структуры алмаза (рис.6.7) можно увидеть такую плоскость.
Элементарная ячейка структуры алмаза – это г.ц.к. ячейка, внутри которой есть еще 4 атома два на высоте 1/4 и два на высоте 3/4; атомы помещаются в центрах октантов, на которые мысленно можно разбить куб, проведя плоскости через середины граней (рис.6.7).
Компоненты скольжения плоскости "d" направлены также вдоль диагонали элементарного параллелограмма, расположенного в плоскости отражения, но величина переноса составляет 1/4 длины диагонали:
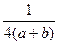 ;
; 
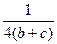 ;
; 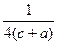

Рис. 6.7. Плоскость скользящего отражения (d) в структуре алмаза.
Дата добавления: 2015-08-21; просмотров: 3594;
