Лекция 2. Структура кристаллов и пространственная

решётка

План лекции

1. Элементарная ячейка, её выбор, метрика.

2. Кристаллическая структура материалов.

3. Ретикулярная плотность сетки.

4. Кристаллографические символы узлов, плоскостей и направлений в кристаллах кубической сингонии.

Расстояния между частицами в большинстве кристаллических веществ составляют несколько десятых долей нанометра, поэтому даже на длине в 1 мм в кристалле располагается ~10⁷ частиц, что практически можно считать бесконечным числом.

Кратчайшее из возможных расстоя­ний между одинаковыми точками в ряду называется элементарной (крат­чайшей) трансляцией или периодом идентичности (рис. 2.1); иногда употреб­ляют названия период трансляции или параметр ряда.

а

Рис 2.1. Симметричный бесконечный ряд с трансляцией а

Если сдвинуть точки бесконечного ряда на один период идентичности вдоль направления трансляции, то все одинаковые точки передвинутся на одинаковые расстояния, ряд совме­стится сам с собой, так что вид его не нарушится. Так производится симмет­ричное преобразование: ряд симмет­рично сдвигается на один период тран­сляции а. Симметричное преобразова­ние, с помощью которого точка повто­ряется в пространстве, называется пре­образованием с помощью трансляции или просто трансляцией. Повторяя ка­кую-либо точку с помощью трансля­ции, получим бесконечный периодиче­ский ряд идентичных точек на расстоя­ниях а, 2а, За, ..., па. Характеристикой этого ряда является кратчайшая тран­сляция а. Одинаковые точки, связан­ные между собой трансляциями а в бесконечном ряду, называются узлами ряда.

2.1. Элементарная ячейка, её выбор, метрика

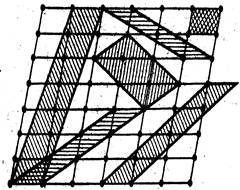
Параллелограммы, вершины которых являются узлами, называют­ся ячейками сетки. Плоскую сетку можно определить любой парой основ­ных трансляций, не лежащих на одной прямой (рис. 2.2, а). Выбор такой пары основных параметров плоской сетки не однозначен. Принято выбирать элементарные трансляции именно те, которые лучше всего отражают сим­метрию сетки.

Выберем в плоской сетке элементар­ную ячейку; повторяя ее с помощью одинаковых трансляций, мы получим плоскую сетку, заполняющую всю плоскость без промежутков. Элемен­тарную ячейку можно выбирать по-разному (рис. 2.2, б), но принято выби­рать ее так. чтобы она удовлетворяла следующим условиям:

1)наилучшим образом отражала симметрию сетки;

2)имела бы прямые углы, если это можно;

3)обладала бы наименьшей площадью.

а	б
в
Рис. 2.2. Плоская сетка: а — различные основные трансляции; б — различные элементарные ячейки; в — примитивная элементарная ячейка, построенная на двух кратчайших трансляци­ях и хорошо отражающая симметрию сетки.

Примитивной элементарной ячейкой называется ячейка, внутри которой нет узлов (рис. 2.2., в).

Число узлов на единицу площади называется рети­кулярной плотностью сетки.

Таким образом, плоскую сетку мож­но определить тремя способами:

1) как пару элементарных неколлинеарных трансляций, или

2) как систему эквивалентных узлов, которые могут быть получены один из другого с помощью параллельных переносов, или

3)как систему одинаковых элементарных ячеек, прилегающих друг к другу, заполняющих плоскость без промежутков и совмещающихся друг с другом с помощью параллельных переносов.

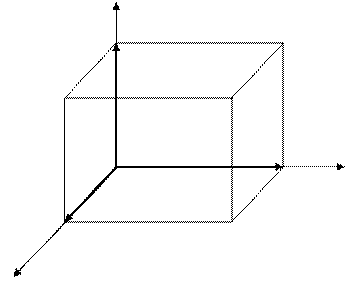
Параллелепипед, построенный на трех элементарных трансляциях a, b, c называется элементарным паралле­лепипедом или элементарной ячейкой.

Набор элементарных углов α, β, γ и элементарных трансляций a, b, c называется метрикой (рис. 2.3)

α   β γ z y x     c b a

Рис. 2.3. Элементарный параллелепипед

Выбор основных трансляций в структуре кристалла очень важен, по­тому что ими определяются кристал­лографические системы координат. Итак, пространственная решетка - это бесконечное трехмерное периоди­ческое образование, или, точнее, это геометрическое построение, с помощью которого в кристаллическом простран­стве выявляются одинаковые точки. Структура кристалла - это кон­кретное расположение частиц в про­странстве.

Пространственная решетка – это способ представления периодичности повторения в пространстве отдельных материальных частиц или групп час­тиц (или «пустых мест» между части­цами).