Еще примечательно то, что хотя за основу для построения схем была взята минимальная ДНФ, ее схемная реализация оказалась тем не менее самой неэкономичной из всех.

Противоречия здесь нет. Поэтому практические оценки в единицах корпуса имеют не очень много общего с теоретическими оценками сложности, принятыми в булевой алгебре. Вид выражения, наиболее экономичного в каком-то техническом базисе, может существенно отличаться от вида минимальной ДНФ, и полученную в результате минимизации ДНФ схемотехник часто склонен рассматривать не как окончательный результат, а лишь как полуфабрикат, с которым можно еще поработать. Отсюда не следует, что минимизация не нужна вообще: чем компактнее выражение, тем легче обрабатывать его дальше.

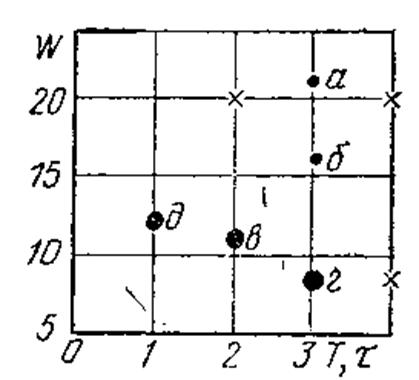
Рис. 2.6. Соотношение величин задержек Т и аппаратурных затрат № схем, изображенных на рис. 2.5

Все сказанное об особенностях поиска схемы относится не только к синтезу схемы по заданному логическому выражению. То же самое можно сказать и о процессе построения более сложных блоков из микросхем средней и большой интеграции. Слабо алгоритмизированный, поисковый, изобретательский стиль работы характерен для всех этапов функционально-логического проектирования цифровой аппаратуры.

Нетрудно видеть, что на рис. 2.6 схемы а и б хуже, чем схема г. Допустим, что преобразовав (2.1) еще несколькими способами, удалось получить схемы, помеченные на рис. 2.6 крестиками. Все эти схемы также оказываются плохими, поскольку для каждой из них существует хотя бы одна схема, которая лучше нее или по Т, или по W, или по обоим показателям сразу. Этого нельзя сказать только о группе схем, образующей «лево-нижнюю» границу всего множества схем, т. е. о схемах д, в, г. При переходе от д к в и от в к г на каждом шаге получается выигрыш в аппаратуре, но проигрыш в скорости. Эти объекты лучше любых других объектов, расположенных выше них и правее, но между собой по характеристикам Т и W они несравнимы. Такая группа объектов называется множеством объектов, оптимальных по Парето.

Введение в обиход разработчика понятия Парето-оптимального множества удобно потому, что при всех реально используемых формулировках задания наилучшим решением всегда оказывается одна из точек множества Парето. Число Парето-оптимальных объектов обычно существенно меньше числа всех вариантов объекта, поэтому работать с множеством Парето заметно проще. Можно выделить Парето-оптимальное множество объектов и по трем характеристикам, добавив к Т и W еще, например, потребляемую мощность P.