Диференціальні рівняння руху матеріальної точки
Диференціальні рівняння руху – це рівняння, які містять похідні та описують рух заданої матеріальної точки.
Вигляд указаних рівнянь залежить від способу описування руху. Нехай матеріальна точка має масу т і рухається під дією сили 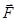 . Розглянемо векторний, координатний і натуральний способи описування руху.
. Розглянемо векторний, координатний і натуральний способи описування руху.
А) Диференціальне рівняння руху матеріальної точки у векторній формі має вигляд:
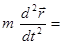
 .
.
При розрахунках це рівняння розглядають разом із початковими умовами руху, які визначають початкове положення і початкову швидкість точки.
Початкові умови руху точки у векторній формі мають вигляд:
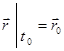 ,
, 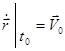 .
.
(початкове положення) (початкова швидкість)
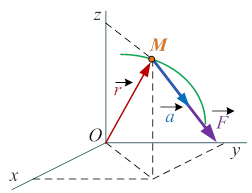
Щоб отримати указане диференціальне рівняння, враховуємо, що при векторному способі описування руху положення матеріальної точки М відносно інерціальної системи відліку визначають за допомогою радіуса-вектора 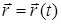 , а її прискорення визначають за формулою , а її прискорення визначають за формулою
 . .
| 
|
Враховуємо також, що сила  , яка діє на точку М, у загальному випадку може залежати від часу t, радіуса-вектора
, яка діє на точку М, у загальному випадку може залежати від часу t, радіуса-вектора 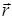 і швидкості
і швидкості 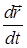 , тобто
, тобто 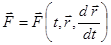 .
.
Отже, за основним законом динаміки отримаємо:
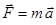 =>
=> 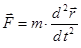 =>
=> 
 .
.
Зазначимо, що указане диференціальне рівняння має другий порядок (оскільки містить похідну другого порядку).
Б) У координатній формі диференціальні рівняння руху матеріальної точки мають вигляд:
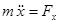 ,
, 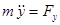 ,
, 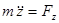 .
.
Тут 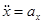 ,
, 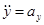 ,
,  є проекціями прискорення
є проекціями прискорення 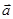 на координатні осі;
на координатні осі;
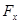 ,
,  ,
, 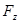 – проекції сили
– проекції сили  , кожна з яких може залежати від часу t, від координат точки та від її швидкості.
, кожна з яких може залежати від часу t, від координат точки та від її швидкості.
Початкові умови руху точки при координатному способі мають вигляд:
початкове положення 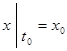 ,
, 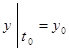 ,
,  ;
;
початкова швидкість 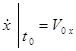 ,
,  ,
, 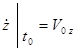
В) При натуральному способі описування руху диференціальні рівняння руху матеріальної точки мають вигляд:
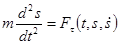 , ,
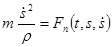 , ,
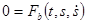 ,
де т – маса точки, ,
де т – маса точки,
| 
|
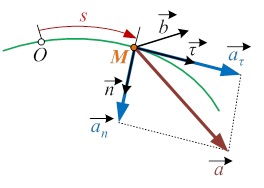
s – дугова координата точки, 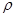 – радіус кривини траєкторії,
– радіус кривини траєкторії,
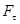 ,
, 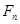 ,
,  – проекції сили
– проекції сили  на дотичну
на дотичну 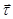 , на головну нормаль
, на головну нормаль  та на бінормаль
та на бінормаль 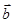 відповідно.
відповідно.
Початкові умови руху точки при натуральному способі мають вигляд:
початкове положення 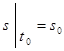 , початкова швидкість
, початкова швидкість 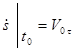 .
.
Дата добавления: 2015-08-21; просмотров: 6098;
