Двусторонние и односторонние поверхности
План
- Двусторонние и односторонние поверхности
- Определение поверхностного интеграла І типа
- Вычисление поверхностного интеграла І типа
Двусторонние и односторонние поверхности
Пусть поверхность определена явным образом с помощью уравнения
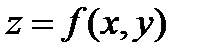 .
.
Такая поверхность не ограничивает никакое тело, она является незамкнутой. Здесь можно определить верхнюю и нижнюю стороны поверхности. Если поверхность ограничивает какое-то тело, то для нее можно определить внутреннюю и внешнюю стороны.
Рассмотрим гладкую поверхность 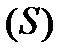 , которая может быть замкнутой или ограниченной кусочно-гладким контуром. В каждой точке такой поверхности к ней можно провести касательную плоскость. Возьмем на поверхности некоторую точку
, которая может быть замкнутой или ограниченной кусочно-гладким контуром. В каждой точке такой поверхности к ней можно провести касательную плоскость. Возьмем на поверхности некоторую точку 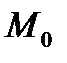 , построим в ней нормаль определенного направления. Построим на поверхности замкнутый контур
, построим в ней нормаль определенного направления. Построим на поверхности замкнутый контур 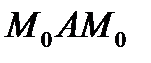 , который не пересекает границ поверхности. Будем обходить этот контур, строя в каждой его точке нормаль к поверхности (непрерывно изменяя нормаль). При возвращении в точку
, который не пересекает границ поверхности. Будем обходить этот контур, строя в каждой его точке нормаль к поверхности (непрерывно изменяя нормаль). При возвращении в точку 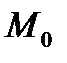 возможны два случая:
возможны два случая:
· Мы возвратимся в 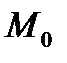 с тем же направлением нормали, с каким выходили из нее;
с тем же направлением нормали, с каким выходили из нее;
· Мы возвратимся в 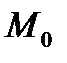 с противоположным направлением нормали.
с противоположным направлением нормали.
Если для поверхности всегда имеет место первый случай, то поверхность является двусторонней, если для поверхности возможен и второй случай, то поверхность односторонняя. Примером односторонней поверхности является лист Мёбиуса.
Дальше рассматриваются лишь двусторонние поверхности.
Определение. Совокупность всех точек поверхности с определенными направлениями нормалей в них называется стороной поверхности.
Пример. Пусть поверхность задана с помощью уравнения 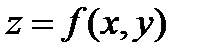 , функция
, функция 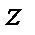 непрерывна в некоторой области
непрерывна в некоторой области 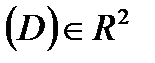 , и
, и 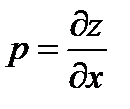 ,
, 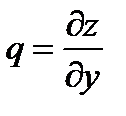 - непрерывны в
- непрерывны в 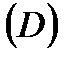 . Тогда направляющие косинусы нормали к поверхности имеют вид:
. Тогда направляющие косинусы нормали к поверхности имеют вид:
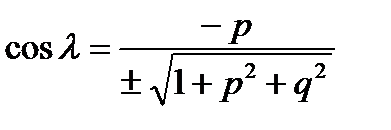 ,
, 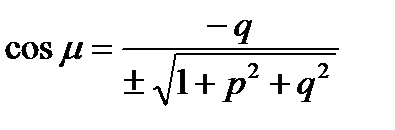 ,
, 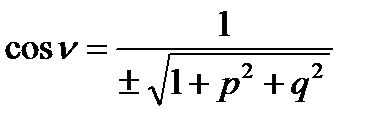 .
.
Если 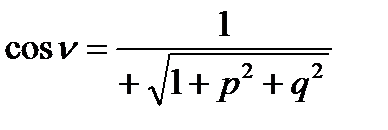 , то угол между поверхностью и осью OZ меньше
, то угол между поверхностью и осью OZ меньше 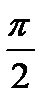 , определена верхняя сторона поверхности, для
, определена верхняя сторона поверхности, для 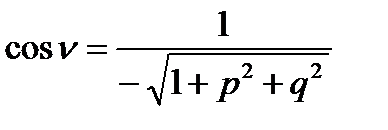 определяется нижняя сторона поверхности.
определяется нижняя сторона поверхности.
2. Определение поверхностного интеграла І типа
Пусть  - двусторонняя гладкая или кусочно-гладкая поверхность. На
- двусторонняя гладкая или кусочно-гладкая поверхность. На 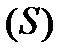 определена функция
определена функция 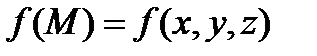 . Разобьем
. Разобьем 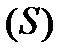 с помощью произвольных кусочно-гладких кривых на части
с помощью произвольных кусочно-гладких кривых на части 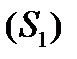 ,
, 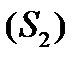 , ...,
, ..., 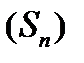 . Возьмем произвольно в каждой части
. Возьмем произвольно в каждой части 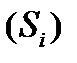 точку
точку 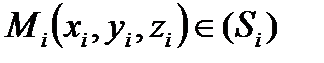 и вычислим
и вычислим 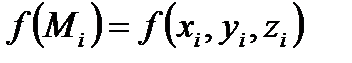 . Значение
. Значение  помножим на площадь
помножим на площадь 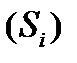 , которую обозначим
, которую обозначим 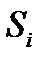 , тогда сумма
, тогда сумма
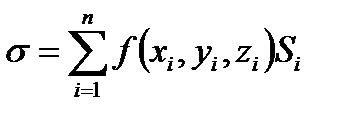
называется интегральной суммой для поверхностного интеграла І типа.
Обозначим:
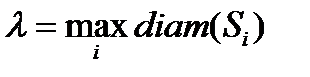 .
.
Определение. Если существует
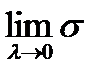 ,
,
который не зависит ни от способа разбиения 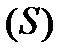 на части, ни от выбора промежуточных точек
на части, ни от выбора промежуточных точек 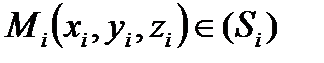 , то этот предел называется поверхностным интегралом І типа от функции
, то этот предел называется поверхностным интегралом І типа от функции 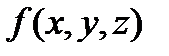 по поверхности
по поверхности 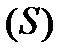 и обозначается
и обозначается
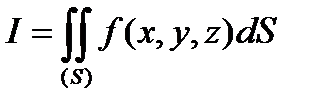 .
.
3. Вычисление поверхностного интеграла І типа
Пусть поверхность 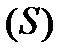 определяется параметрично:
определяется параметрично:
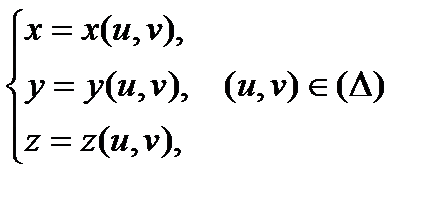 .
.
Обозначим:
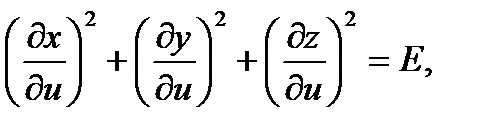
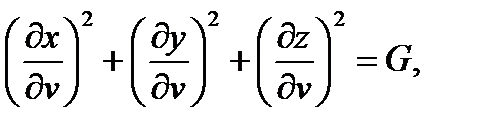
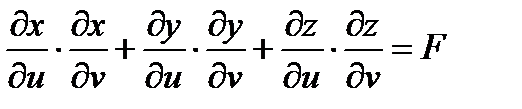 .
.
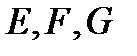 называются гауссовыми коэффициентами поверхности.
называются гауссовыми коэффициентами поверхности.
Пусть 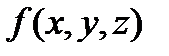 определена в точках поверхности
определена в точках поверхности 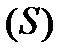 и ограничена, тогда:
и ограничена, тогда:
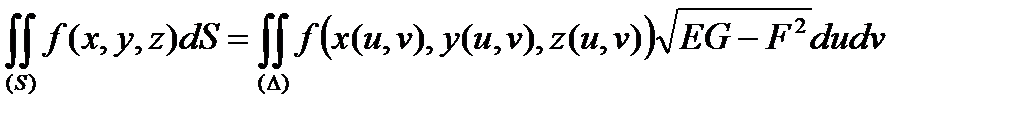 .
.
Пусть теперь поверхность 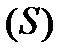 определена:
определена: 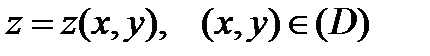 . Если
. Если 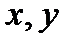 рассмотреть как параметры, то параметрическое задание этой поверхности будет иметь вид:
рассмотреть как параметры, то параметрическое задание этой поверхности будет иметь вид:
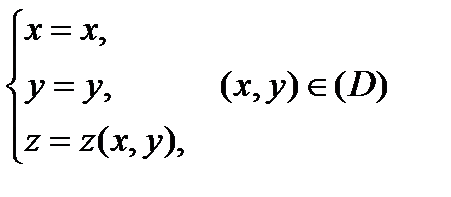 .
.
Для такого задания поверхности:
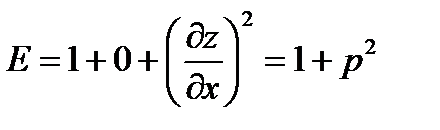 ,
, 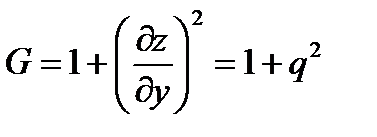 ,
, 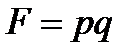 ,
,
Тогда
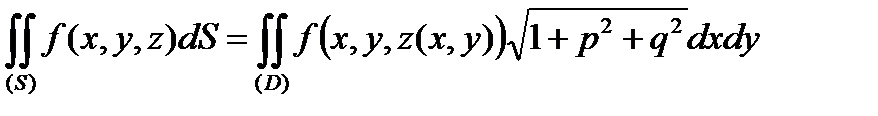 .
.
Задание. Вычислить
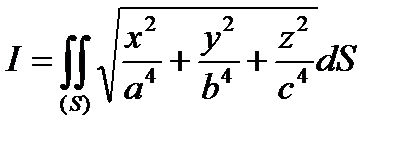 ,
,
где 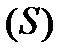 - эллипсоид
- эллипсоид  . Параметрическое задание эллипсоида:
. Параметрическое задание эллипсоида:
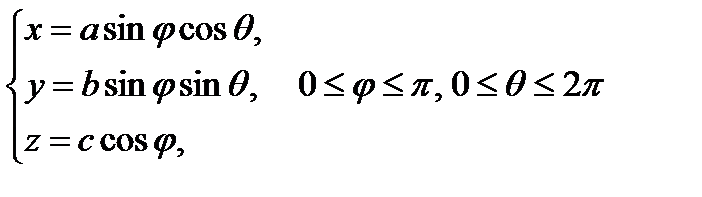 .
.
При правильном вычислении результат должен равняться: 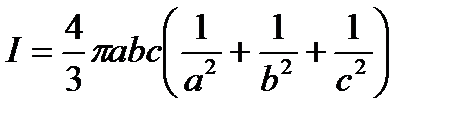 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Формула Гріна | | | Двобічні і однобічні поверхні |
Дата добавления: 2015-08-21; просмотров: 2064;
