Преобразования Галилея и Лоренца.
Удивительные следствия принципа постоянства скорости света часто иллюстрируют на примере пассажира, который едет в вагоне сверхбыстрого поезда.
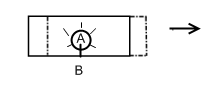
Наблюдатель в вагоне имеет лампу, установленную в середине вагона. Для наблюдателя А, движущегося вместе с вагоном, видно, что оба сигнала выходят из середины вагона и распространяются в обе стороны, достигая обоих концов в один и тот же момент. Скорость света одинакова для лучей. Расстояния, ими проходимые, также одинаковы. Наблюдатель В должен увидеть левый сигнал быстрее, чем правый, т.к. вагон перемещается слева направо. Для него оба сигнала приходят не одновременно, а с некоторой разностью во времени. Кто прав? Согласно теории относительности, оба заключения правильны. Одновременность двух пространственно разделенных событий не является абсолютным свойством самих событий, а лишь следствие их способа рассмотрения.
Рассмотрим, каким условиям должны удовлетворять преобразования пространственных координат и времени при переходе из одной системы отсчета к другой. Если принять предположение классической механики об абсолютном характере расстояний и длин, то уравнения будут иметь вид:
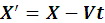
Эти уравнения называются преобразованиями Галилея.
Если же преобразования должны удовлетворять также требованию постоянства скорости света, то они описываются уравнениями Лоренца. Если система отсчета движется вдоль оси X, то координаты и время в движущейся системе выражаются уравнениями:
.
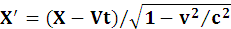
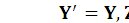
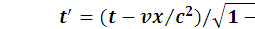Движущаяся линейка будет короче покоящейся, и тем короче, чем быстрее она движется. Пусть начало линейки находится в начале координат, и ее абсцисса 
, а конец (в движущейся системе). В неподвижной системе
, 
,
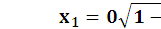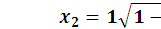Т.е. длина линейки в неподвижной системе составит 
длины в движущейся системе.
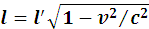
Интервал времени между двумя событиями в двух системах отсчета будет разным (x=0)
.
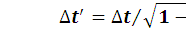Из уравнений следует, что вследствие движения наблюдателей друг относительно друга они, измеряя интервалы времени между двумя данными событиями, получают разные результаты.
Если V <<с, то уравнения Лоренца переходят в уравнения мы встречаемся со скоростями, значительно меньшими скорости света, поэтому изменения, которые требует вносить теория относительности, крайне незначительны. Например, даже для ракеты, летящей со скоростью 50 000 км/ч, v/c= 5٠10-5
Эффект замедления времени на движущейся ракете является свойством пространства и времени. Наблюдатель на ракете ничего странного не замечает. Представляет интерес «парадокс близнецов» для иллюстрации эффектов теории относительности. Один «близнец» отправляется в космическое путешествие, другой остается на Земле. В равномерно движущемся с огромной скоростью космическом корабле темп времени замедляется, все процессы происходят медленнее. Космонавт, вернувшись, оказывается более молодым, чем оставшийся на Земле.
Другой пример – наблюдения над элементарными частицами, названными µ-мезонами (мюонами). Средняя продолжительность существования таких частиц – 2 мкс, некоторые из них, образуясь на высоте 10 км, долетают до поверхности Земли. Хотя при средней «жизни» в 2 мкс они могут проделать путь только 600 м. Продолжительность существования мюонов определяется по-разному для разных систем отсчета. С «их» точки отчета, они живут 2 мкс, с нашей, земной – значительно больше.
Дата добавления: 2015-08-21; просмотров: 1846;