Расчет равновесий для систем, отклоняющихся от законов Рауля и Генри

(для неидеальных растворов).

Таких систем большинство и для них необходимо знать термодинамические параметры всех компонентов в стандартном состоянии. За стандартное состояние растворителя принимается стандартное состояние чистого растворителя (при стандартных условиях). За стандартное состояние растворенного вещества принимается фиктивное или гипотетическое состояние в идеальном растворе, когда активность этого вещества равна 1, но с теми же термодинамическими параметрами, которыми вещество обладает в бесконечно разбавленном растворе.

В реальных растворах активность соответствует мольной доле только при бесконечном разбавлении:

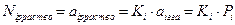
K_i – константа распределения (константа фазового равновесия для i-го компонента).

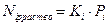
Для определения K_i проводят экспериментальные исследования в области очень разбавленных растворов, постепенно снижая концентрацию раствора N_i.

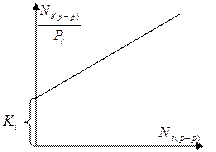
Эта зависимость будет прямой линией только при концентрациях близких к 0.

Из найденного графически значения K_i рассчитывают парциальные давления пара i-ого компонента над раствором, где его активность равна 1.

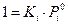
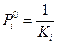
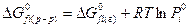
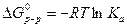
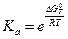
Если в реакции имеются твердые компоненты, то принимают, что их активность равна 1 и 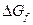равна 0, поэтому их не учитывают. Для растворителя необходимо учитывать поправку, которая учитывает, что активность растворителя равна отношению парциального давления пара над данным раствором и над чистой жидкостью.

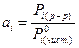
Теоретическое описание равновесие довольно сложное. Реально константы равновесия определяются не теоретически, а экспериментально. Особенно важно, если отсутствуют справочные данные по величинам термодинамических функций образования.