Равновесие в случае реальных газов
Для газов верно следующее:
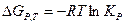
Это выражение соблюдается только в том случае, если газы идеальные. Если же газ реальный, то необходимо использовать уравнение:
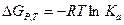 ,
,
где а – активность.
Активностью называется отношение парциального давления газа в данном и стандартном состояниях.
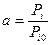
Под стандартном состоянием газа или пара принимается его состояние в виде идеального газа при стандартных условиях Давление – 1 атм или 0,103 МПа, Температура – 298,15 К. Изначально все выражения были выведены для атмосфер. Поскольку в технической системе единиц P0 = 1 атм, поэтому активность идеального газа будет равна его парциальному давлению. Так как, константа равновесия:
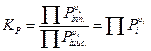
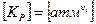 .
.
Перевод осуществляется по формуле:
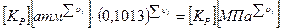 .
.
Для реальных газов необходимо использовать только:
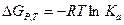 ,
,
Так как, 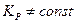 .
.
Пример: экспериментальные данные по синтезу аммиака при 450 оС и различных давлениях.
| Робщ. | 1 | 10 | 30 | 50 | 100 | 300 | 600 | 1000 |
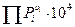
| 41,1 | 42.9 | 45 | 47,1 | 51,8 | 76,8 | 163,8 | 519,8 |
Рост константы с ростом давления является следствием отклонения газообразной системы от состояния идеального газа. Чем выше давление, тем больше межмолекулярные силы в системе и больше будет изменяться константа.
Для реальных газов соотношение 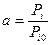 не выполняется.
не выполняется.
Ван-Лаар пытался вывести все уравнения для всех реальных газов, оказалось, что уравнения вывести нельзя в широком интервале давлений.
Пытались при выводе уравнения энергии Гиббса для смеси реальных газов использовать приближенные уравнения состояния, например уравнение Ван-дер-Ваальса, но оказалось, что применять практически такие уравнения сложно из-за сложного математического выражения.
Льюис в 1901 году предложил уравнения, которые нашли очень широкое применение при исследовании реальных систем. Он заменил в уравнении активности парциальное давление на другие переменные и ввел понятие фугитивности (летучести).
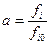
Тогда, активность реального газа равна отношению фугитивностей в данном и стандартном состояниях. За стандартную фугитивность принята фугитивность газа в его идеальном состоянии и стандартном давлении – 1 атмосфера: 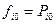 .
.
При низких давления, то есть при состояниях близких к идеальному газу: 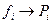 .
.
Для реальных газов:
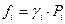 ,
,
γi – коэффициент фугитивности (коэффициент активности) – безразмерная величина.
Фугитивность и коэффициент фугитивности зависят от внешних условий и состава газовой смеси. В зависимости от условий, коэффициента активности может быть больше или меньше 1, все будет зависеть от соотношения межмолекулярных сил. Когда силы отталкивания преобладают над силами притяжения (при очень высоких давлениях), коэффициент фугитивности становится больше 1.
Пример: газ – азот. Давление 6000 атм. 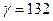 .
.
Коэффициент фугитивности характеризует степень отклонения газа от идеальности.
Связь между активностью и парциальным давлением:
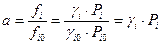
Коэффициент фугитивности находят по принципу соответственных состояний. Согласно которому, знание коэффициента фугитивности для реальных газов являются одинаковыми, если газы находятся при одинаковых приведенных температурах и давлениях.
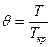
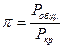
Для таких газов, как водород, гелий, неон:
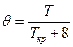
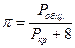
Тогда такие параметры называются псевдокритическими.
Изотерма Вант-Гоффа для реальных газов преобразуется в вид:
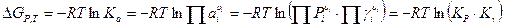 .
.
Алгоритмы нахождения константы равновесия Kp для реальной газовой смеси:
1. Сначала находится изменение энергии Гиббса как для идеальных газов: 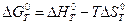 .
.
2. 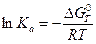 ;
; 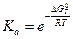 .
.
3. По значению приведенных параметров находится коэффициент фугитивности для всех компонентов. Затем рассчитывается Kγ.
4. Вычисляется 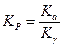 .
.
Дата добавления: 2015-08-14; просмотров: 1528;
