Теорема Чебышева

Основная форма закона больших чисел.

Рассмотрим последовательность попарно независимые случайные величины х₁,х₂…….х_n. Пусть все они имеют математическое ожидание и дисперсии. M[x₁], D[x₁] и средняя арифметическая из первых n-величин.

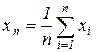
Распишем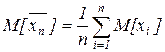

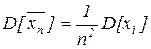. Пусть все дисперсии x_n ограничены числом с, 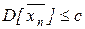, тогда 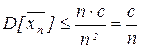. Отсюда видно, что дисперсия от среднего → 0 при n → ¥. Применяя к 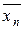неравенство Чебышева:

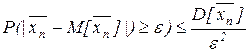или заменим .

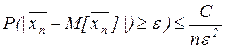Правая часть неравенства ® 0, при n ® ¥, а левая неотрицательна, потому из данного неравенства следует что 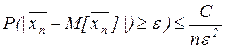, при n ® ¥

,

.

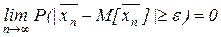Таким образом , теорема Чебышева утверждает, что если рассматривается довольно большое число попарно независимых случайных величин имеющих ограниченные дисперсии , то почти достоверно можно считать, что средняя арифметическая случайной величины сходятся по вероятности со средней арифметической их математического ожидания.

Частный случай – все случайные величины имеют одно и тоже M[x], тогда

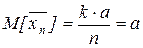M[x]=a,

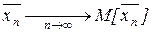, в частном случае