Корреляционные зависимости
Две случайные величины х и у находятся в корреляционной зависимости, если изменение одной из величин влечет за собой изменение закона распределения другой. Для характеристики зависимости между случайными величинами вводят понятие корреляционного момента или ковариации. Корреляционным моментом случайной величины х и у называется математическое ожидание произведения отклонений этих величин от их математических ожиданий
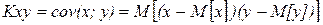 ,
,
Для дискретной случайной величины (отношение) ковариация вычисляется
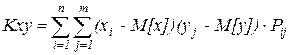 (1)
(1)
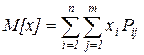 (2)
(2) 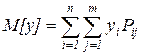 (3)
(3)
Для непрерывных случайных величин
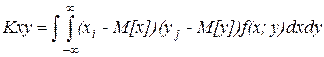 (4)
(4)
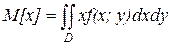 (5)
(5)
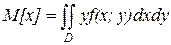 (6)
(6)
Из формулы (4) можно получить более простую формулу.
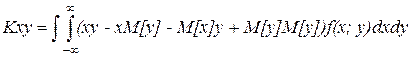
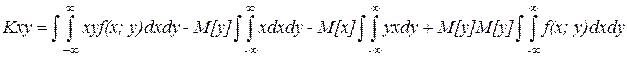
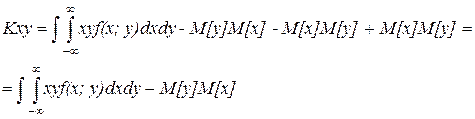
Получим
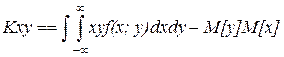 (7)
(7)
Теорема №1 Если случайные величины х и у независимы то их cov(x;y)=0
Доказательство: для непрерывной величины.
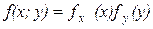
в формуле 4 заменим
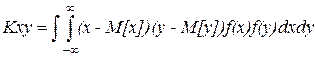
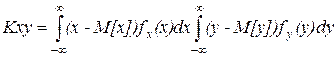
центральный момент первого порядка равен нулю, следовательно и выражение равно нулю. Для независимых случайных величин необходимо чтобы cov=0, но обратно не верно.
Если ковариация двух случайных величин отлична от нуля - это есть признак зависимости между ними. cov характеризует не только зависимость величинами , но и их рассеивание. Если одна из величин весьма мало отклоняется от своего математического ожидания , то есть почти неслучайно, то cov – будет мала, какой бы тесной зависимостью не были бы связаны эти величины. Поэтому между случайными величинами вводят безразмерный коэффициент корреляции.
Дата добавления: 2015-08-14; просмотров: 687;
