Реализации и перспективы квантовой информатики.

Толчком к ускоренному развитию квантовой информатики послужило открытие в конце ХХ в. ряда примеров квантовых алгоритмов для решения задач, которые либо существенно ускоряют решение, либо неразрешимы в рамках классических алгоритмов. Известными примерами таких алгоритмов для квантовых компьютеров являются следующие [50;51]:

Алгоритм Л. Гровера связан с задачей нахождения в неотсорти-рованной базе данных ее некоторого конкретного элемента. Данная задача, фактически, равносильна нахождению решения уравнения f(x)=1, где f(x) – булева функция от n переменных. Классический алгоритм решения данной задачи требует прямого перебора всех N =2ⁿ вариантов. Квантовый алгоритм Гровера дает ~ 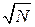, т.е. обеспечивает существенное так называемое «квадратичное» снижение машинного времени перебора вариантов.

Алгоритм Д.Дойча-Р.Джозса заключается в определении, является ли булева функция f( 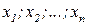) постоянной (т.е. принимающей значение либо 0, либо 1 при любых значениях аргументов) или сбалансированной (когда для половины области определения функция принимает значение 0, а для другой половины 1). Для решения этой задачи по классическому алгоритму требуется 2^{n −1}+1 вычислений функции f. Квантовый алгоритм Дойча-Джозса дает верный ответ за одно вычисление значения функции f.

Алгоритм П. Шора. Задачи, алгоритм решения которых имеет экспоненциальную сложность [52], не под силу современным компьютерам. Классическим примером является задача факторизации (разложения на простые множители) целого n-разрядного числа. Самые быстрые классические алгоритмы решают эту задачу за ~ exp (n log n) 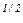шагов, т.е. имеют экспоненциальную сложность и, например, для разложения на множители случайно выбранного числа, имеющего n=1000 десятичных знаков, необходимо ~ 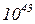шагов, что потребует машинное время, превышающее возраст Вселенной. 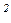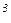Квантовый алгоритм для проведения данной операции требует ~ n log n шагов и, как видим, обладает полиномиальной сложностью. В частности, для решения данного примера квантовому алгоритму потребуется ~ 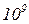шагов и машинное время менее 1 сек. Комментарии, как говорится, излишни.

В то же время установлено, что многие алгоритмы, выполняемые неплохо на классических компьютерах, не ускоряются на квантовом [46]. Тем не менее, следует указать причины ускорения процесса решения задач на квантовом компьютере, которые, судя по всему, лежат в квантовой природе кубитов, что приводит к следующим феноменам:

1. Гильбертово пространство состояний квантовой системы из n кубитов имеет гораздо бóльшую размерность, равную 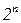. Физически это означает, что система имеет 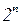базовых состояний, а состояние компьютера описывается суперпозицией из этих 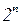базовых состояний. Это приводит к коллективному эффекту, поскольку воздействие на какой-либо кубит системы одновременно изменяет все 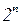базовых состояний. Этот феномен носит название квантового параллелизма, который во многих случаях способствует ускорению решения поставленной задачи.

2. Вычислительный процесс носит характер интерференции, так как амплитуды базисных состояний волновой функции являются комплексными числами. Поэтому квантовый компьютер можно рассматривать как сложное интерференционное устройство, в котором интерференция состояний создает вычислительную мощь компьютера, по аналогии с увеличением амплитуды волн при интерференции света.

Естественно, прогресс в области квантовой информатики затрагивает широкие области возможных приложений, среди которых, традиционно, выделяются криптография и системы связи.

Среди криптосистем наиболее известны системы с открытым ключом (RSA-система: Rivest, Sharnir, Adieman; 1977) и системы с ключом одноразового пользования (Vernam, 1935) [46].

Сразу отметим, что в основе системы RSA лежит предположение о том, что решение математической задачи о разложении больших чисел на простые множители на классических компьютерах невозможно; оно требует экспоненциально большого числа операций и астрономического времени. Квантовый алгоритм Шора дает возможность вычислить простые множители больших чисел за практически приемлемое время и взломать шифры RSA криптосистем, т.е. для RSA-систем квантовый компьютер – плохая новость.

Для криптосистем с ключом одноразового пользования квантовые методы связи оказываются хорошей новостью: они позволяют обнаружить наличие подслушивания при передаче ключа. Эта возможность основана на квантовом принципе неопределенности Гейзенберга, который гласит, что всякое измерение изменяет состояние измеряемой квантовой системы. Поэтому, квантовые методы обеспечивают гарантированную секретность ключа одноразового пользования.

Квантовые каналы связи позволяют реализовать «плотное квантовое кодирование» информации, поскольку с помощью одного кубита можно передать 2 бита информации. С другой стороны, возможна передача неизвестного квантового состояния ("квантовая телепортация") по классическому каналу, если абоненты связи предварительно поделили коррелированную пару квантовых частиц. Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 4 кубита: источник, приёмник и два вспомогательных. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удаленных на большое расстояние. Отметим, что потенциальные возможности применения этих феноменов до конца не выяснены.

По поводу конкретной реализации квантового компьютера пока более-менее достоверным выглядит сообщение из Национального института стандартов и технологий (США, 2009), где, впервые, удалось собрать программируемый квантовый компьютер, состоящий из 2 кубит. По оценкам [46], технологии с атомным разрешением имеют высокий уровень зрелости и работа с отдельными атомами является экспериментальной реальностью. Тем не менее, предстоит пройти большой путь до создания полномасштабного (10³-10⁴кубитов) квантового компьютера и пока неясно, какой способ построения квантового компьютера окажется предпочтительным.

Библиография к части 3.

1. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов.– М.: Наука, 1974. – 415 с.

2. Бонгард М.М. Проблема узнавания. – М.: Наука, 1967. – 320 с.

3. Искусственный интеллект. Справочник. В 3-х кн. Кн. 2. Модели и методы / Под ред. Д.А. Поспелова. – М.: Радио и связь, 1990. – 304 с.

4. Мулен Э. Кооперативное принятие решений: Аксиомы и модели. – М.: Мир, 1991. – 464 с.

5. Мазуров В.Д. Метод комитетов в задачах оптимизации и классификации. – М.: Наука, 1990. – 248 с.

6. Фирстов В.Е. Кибернетическая концепция и математические модели управления дидактическими процессами при обучении математике в школе и вузе // Монография. – Саратов: Издательский Центр «Наука», 2010. – 511 с.

7. Лидл Р., Пильц Г. Прикладная абстрактная алгебра // Под ред. Л.Н. Шеврина. – Екатеринбург: Изд-во Урал. ун-та, 1996. – 744 с.

8. White H.C., Boorman S.A., Breiger R.L. Social structure from multiple networks, I: blockmodels of roles and positions // Amer. J. Sociol., 1976, v. 81. – P. 730-780.

9. White H.C.,Boorman S.A. Social structure from multiple networks, II: role structures // Amer. J. Sociol., 1976, v. 81. – P. 1384-1466.

10. Ньюэлл А., Шоу Дж.С., Саймон Г.А. Процессы творческого мышления // В кн.: Психология мышления.– М.: Прогресс, 1965. – С. 500-530.

11. Гелернтер Г. Реализация машины, доказывающей геометрические теоремы // Вычислительные машины и мышление. – М.: Мир, 1967. – С. 145-164.

12. Андельсон-Вельский Г.М., Арлазаров Б.Л., Битман А.Р., Донской М.В. Машина играет в шахматы.– М.: Наука, 1983. – 207 с.

13. Искусственный интеллект. Справочник. В 3-х кн. Кн. 1. Системы общения и экспертные системы: / Под ред. Э.В. Попова. – М.: Радио и связь, 1990. – 464 с.

14. Вагин В.Н., Кикнадзе В.Г. Дедуктивный вывод на семантических сетях в системах принятия решения // Изв. АН СССР: Техническая кибернетика, 1984, № 5. – С. 104-120.

15. Глушков В.М. Кибернетика. Вопросы теории и практики.– М.: Наука, 1986. – 488 с.

16. Поспелов Д.А. Логико-лингвистические модели в системах управления.– М.: Энергоиздат, 1981. - 231 с.

17. Поспелов Г.С. Системный анализ и искусственный интеллект.– М.:Изд-во АН СССР, 1980. – 47 с.

18. Пушкин В.Н. Оперативное мышление в больших системах. – М.-Л.: Энергия, 1965. – 375 с.

19. Космическое оружие: дилемма безопасности. Под ред. Е.П. Велихова, Р.З. Сагдеева, А.А. Кокошина.– М.: Мир, 1986. – 182 с.

20. Малинецкий Г.Г. Математические основы синергетики: Хаос, структуры, вычислительный эксперимент.– М.: Издательство ЛКИ, 2007. – 312 с.

21. Фейгенбаум М. Универсальное поведение в нелинейных системах // УФН, 1983, т. 141, №2. – С. 343-374.

22. Анохин П.К. Очерки по физиологии функциональных систем.– М.: Медицина, 1975. – 447 с.

23. Марютина Т.М., Ермолаев О.Ю. Введение в психофизиологию,– М.: Московский психо-социальный ин-т: Флинта, 2004. – 400 с.

24. Зиман Э., Бьюнеман О. Толерантные пространства и мозг // В кн. На пути к теоретической биологии. – М.: Мир, 1970. – С. 134-144.

25. Пенроуз Р. Новый ум короля: О компьютерах, мышлении и законах физики. – М.: Едиториал УРСС, 2005. – 400 с.

26. Малинецкий Г.Г., Ижикевич Е.М. О возможной роли хаоса в нейросистемах //Доклады РАН, 1992, т. 326, №4. – С. 626-632.

27. Hopfild, J.J. Neural networks and physical systems with emergent collective computational abilities // Proc. Natl. Acad. Sci. USA, 1982, v.79. – P. 2554-2558.

28. Веденов, А.А., Ежов А.А., Книжникова Л.А., Левченко Е.Б., Чернов Ю.Г. Нелинейные системы с памятью и моделирование функций нейронных ансамблей // Интеллектуальные процессы и их моделирование. Под ред. Е.П.Велихова и А.В.Чернавского. – М.: Наука, 1987. – С. 229-248.

29. Гинзбург С.Л. Необратимые явления в спиновых стеклах.– М.: Наука, 1989. – 152 с.

30. Фирстов В.Е. Концепция развивающего обучения Л.С.Выготского, педагогика сотрудничества и кибернетика // Ярославский педагогический вестник, 2008, №4(57). – С.98-104.

31. Фирстов В.Е. Обучение в диалоге: кибернетический аспект // Вестник Саратовского госуд. техн. ун-та, 2007, №4 (28), вып. 1. – С 135-145.

32. Фирстов В.Е.Экспертные системы и информационная концепция развивающего обучения // Ярославский педагогический вестник, 2009, № 1(58). – С.69-73.

33. Косоруков О.А., Мищенко А.В. Исследования операций. – М.: Изд-во «Экзамен», 2005. – 448 с.

34. Занков Л.В. Избранные педагогические труды. – М.: Педагогика, 1990. – 424 с.

35. Рубинштейн С.Л. Основы общей психологии.– СПб.: Питер, 2005. – 713 с.

36. Малинецкий Г.Г., Курдюмов С.П. Синергетика, прогноз и управление риском // Синергетическая парадигма. Нелинейное мышление в науке и искусстве .– М.: Прогресс-Традиция, 2002. – С. 378-405.

37. Архангельский С.И. Лекции по научной организации учебного процесса в высшей школе. – М.: Высшая школа, 1976. – 200 с.

38. Ительсон Л.Б. Математические и кибернетические методы в педагогике. – М.: Просвещение, 1964. – 248 с.

39. Борисенков В.П. Стратегия образовательных реформ в России (1985-2005 гг.) // Педагогика, 2006, №7. – С. 3-16.

40. Стражев В. Пять реформ советской школы // Alma mater (Вестник высшей школы), 2005, №5. – С. 3-17.

41. Национальная доктрина развития образования в РФ (на период 2000-2025 гг.). – Одобрена Правительством РФ от 17.02.2000 г.

42. Малинецкий Г.Г. Выбор стратегии // Компьютерра, №38 (513), 7 октября 2003 г. – С. 25-31.

43. Россия: образование в переходный период // Доклад всемирного банка, 1995. – Всемирный банк: Управление Европы и Центральной Азии, департамент III. Отдел социальных ресурсов. 1995. – 250 с.

44. Бриллюэн Л. Наука и теория информации. – М,: Физматгиз, 1960. – 392 с.

45. Игошин В.И. Математическая логика и теория алгоритмов. – М.: Издательский центр «Академия», 2004. – 448 с.

46. Валиев К.А. Квантовая информатика: компьютеры, связь и криптография // Вестник РАН, 2000, т.70, №8. – С. 688-695.

47. Давыдов А.С. Квантовая механика. – М.: Наука, 1973. – 703 с.

48. Манин Ю.И. Вычислимое и невычислимое. – М.: Советское радио, 1980. – С. 15.

49. Feynman R.P. Simulating physics with computers // Intern. Journal of Theoretical Physics, 1982,.vol.21. №6. – P. 467-488.

50. Квантовые вычисления: за и против. Под ред. В.А. Садовничего. – Ижевск: Издательский дом «Удмуртский университет», 1999. – 212 с.

51. Валиев К.А. Квантовые компьютеры и квантовые вычисления // УФН, 2005, т.175, №1. – С. 3-39.

52. Ахо А., Хопкрофт Дж.,Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. — 535 с.