Кубиты и операции с ними.
Идея квантовых вычислений, впервые высказанная Ю.И. Маниным [48] и Р. Фейнманом [49], состоит в том, что квантовая система, содержащая n двухуровневых элементов – квантовых битов или кубитов – имеет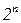 
линейно независимых состояний и, следовательно, по принципу квантовой суперпозиции, пространством состояний такого квантового регистра является 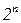-мерное гильбертово пространство. Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером в n кубит может выполнять параллельно 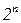операций.
Пусть имеется один кубит. Тогда измерение его состояния в рамках классической механики даст результат 0 или 1, т.к. измеряемый объект в этом случае может находиться только в одном из двух возможных состояний. Однако кубит – квантовый объект и поэтому, вследствие принципа неопределенности Гейзенберга, в результате измерения может быть и 0, и 1 с определенной вероятностью. Если состоянию кубита соответствует 0 (или 1) со стопроцентной вероятностью, то его состояние обозначается кет-вектором Дирака |0> (или |1>), представляя базисные состояния кубита. В общем случае квантовое состояние кубита представляет суперпозицию a|0> + b|1>, где |a|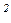 
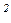и |b| - вероятности измерить 0 или 1 соответственно, как следует из определения волновой функции [47]; a;b 
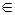C;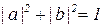 
. Более того, сразу после измерения кубит переходит в базовое квантовое состояние, аналогичное классическому результату.
Пример. Имеется кубит в квантовом состоянии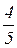 
|0> –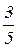 
|1>. В этом случае, вероятность получить в измерении 0 составляет (4/5) 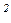= 0,64 = 64%, а 1:(-3.5) 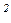= 0,36 = 36%. Т.к. в измерении 0 получился с большей вероятностью, то кубит переходит в новое квантовое состояние 1|0> + 0|1> = |0>, т.е. при следующем измерении данного кубита получится 0 со 100% вероятностью. Это обусловлено тем, что дираковский вектор состояния не зависит от времени, т.е. представляется в виде линейной комбинации векторов базисных состояний с независимыми от времени коэффициентами [47].
Отметим, что реальными двухуровневыми системами, например, является спин ядра или электрона в постоянном внешнем поле, поляризация фотона, оптические уровни энергии и состояния электрона в ионе Са 
[46].
В системе из двух кубитов имеются 4 классических состояния 00;01;10;11 и при измерении они дают вероятность 0 или 1. Базисными квантовыми состояниями в этом случае являются дираковские кет-векторы |00>;|01>;|10>;|11> и в общем случае квантовое состояние данной системы имеет вид a|00> + b|01> + c|10> + d|11> , где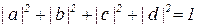 
; a;b;с;d 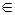Cи теперь |a| 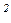– вероятность измерить 00 и т.д.
Пример. Имеется 2-кубитная система в состоянии: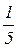 
|00> + 
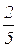|01> +
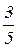+ |10> + 
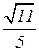|11>. Вероятность получить в измерении состояние 00 равна (1/5) 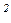= 0,04 =4%; состояние 01 – (2/5) 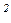= 0,16=16%; состояние 10 – (3/5) 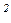= 0,36 = 36%; состояние 11 – ( 
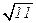/5) 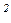= 0,44 = 44%. Т.к. состояние 11 в измерении получилось с наибольшей вероятностью, то данная система переходит в новое квантовое состояние 0|00> + 0|01> + 0|10> + 1|11> = |11>, т.е. при следующем измерении данной квантовой системы получится состояние 11 со 100% вероятностью.
В общем случае у системы из n кубитов имеется 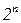классических состояний 000…(n нулей), … 001 (n цифр), …, 111… (n единиц), каждое из которых может быть измерено с вероятностями 0 – 100%. Данные n кубитов образуют квантовый регистр компьютера. В ходе выполнения квантового алгоритма состояния кубитов изменяются согласно плану выполнения алгоритма. Доказано, что любой квантовый алгоритм может быть разложен на последовательность преобразований состояний отдельных кубитов и пар кубитов (1- и 2-кубитовые преобразования, или "вентили") [46].
Таким образом, операция суперпозиции над группой кубитов затрагивает всевозможные значения, которые она может принимать, в отличие от классического бита. Тем самым, открываются широкие возможности для распараллеливания алгоритмов вычислений.
Дата добавления: 2015-08-14; просмотров: 968;