Постановка задач.

Во 2-ой половине XX в. объем экспериментальных знаний о деятельности мозга достиг величины, позволяющей проводить адекватную систематизацию этих знаний в рамках формализованных моделей, среди которых наибольшее предпочтение сейчас отдается нейросетевым моделям. Имеющийся опыт требует, чтобы такие модели воспроизводили наиболее важные особенности деятельности мозга и, прежде всего, его памяти:

1). Ассоциативность и устойчивость ассоциативных связей.Информация об объектах окружающего мира в памяти мозга фиксируется в виде некоторых образов (гештальтов), каждый из которых, в рамках нейросетевой модели, представляется определенным ансамблем нейронов с фиксированной структурой ассоциативных связей между нейронами этого ансамбля. Сам процесс формирования таких нейроансамблей в данном случае выступает как процесс обучения соответствующей нейросети распознаванию определенного объекта, информация о котором поступает из внешнего информационного пространства на входы сети. Довольно часто обучение сети реализуется путем многократной прогонки информации об интересующем объекте по обучаемой сети до тех пор, пока не происходит стабилизация весов ассоциативных связей между нейронами сети, после чего объект достаточно четко идентифицируется и запоминается сетью.

Важно также, чтобы представленный нейросетью образ распознавался по неполной информации, как это наблюдается при естественной деятельности мозга. Иными словами, реальный образ может несколько отличаться от своего «эталонного» образа в памяти сети, но при этом достаточно четко идентифицироваться. Формально это сводится к определению нормы в пространстве образов X, так, что, если существует определенное значение 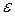>0, для которого

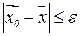, (11.1)

то представленный образ 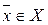можно идентифицировать с эталонным образом 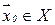, хранящимся в памяти данной сети.

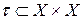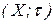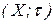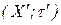
Можно видеть, что неравенство (11.1) в пространстве Х определяет некоторое бинарное отношение , которое рефлексивно и симметрично, и называется отношением толерантности, а пара в этом случае образует толерантное пространство. Если ; 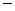два толерантных пространства и при этом отображение 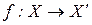сохраняет толерантность, т.е. 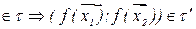, то f – называют толерантным отображением.

Представление о толерантном пространстве впервые появилось в работе О.Бьюнемана и Э.Зимана (1970) [24] именно для описания поведения мозга, когда процесс передачи информации между функциональными элементами структуры мозга описывается посредством соответствующих толерантных преобразований. В этой связи можно привести следующие характерные примеры.

Модель памяти. Известно [23], что нервные волокна идущие к коре мозга, проходят через таламические центры, причем, таламус участвует в формировании практически всех рефлексов, за исключением простейших. Пусть Х – пространство внешних стимулов, а С;Т – пространства, описывающие состояния коры и таламуса. Тогда процесс формирования образов памяти (в таламусе) представляется в виде следующей схемы толерантных отображений

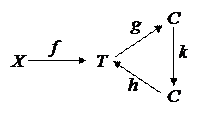
, (11.2)

где f, g, h, k – соответствующие толерантные отображения.

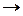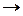Вербальное общение. В этом случае процесс передачи информации происходит по схеме: мысли слова мысли. Пусть M₁;M₂ – пространства мыслей участников общения и С – пространство слов, выражающее мысли М₁. Тогда с помощью толерантных отображений f и g данное общение можно описать схемой: 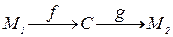, откуда видно (учитывая (11.1)), что уровень понимания мыслей М₁ вторым собеседником будет определяться точностью словесного выражения мыслей С=f(M₁) и его воспроизведением М₂=g(C). Наличие композиции двух толерантных отображений в данном процессе общения, как это прямо следует из (11.1), увеличивает неопределенность передачи информации и именно с этим связана известная проблема некоммуникабельности.

2). Дистрибутивный принцип хранения информации и надежность сети. По имеющимся данным [20;23;25], в мозге за хранение информации о конкретном объекте, как правило, отвечает не отдельный нейрон, а их некоторый структурированный ансамбль, так, что информация об объекте некоторым образом распределена по нейросети. Такой дистрибутивный принцип в управлении информацией, по сравнению с «фон-неймановской» архитектурой современных компьютеров, оказывается намного эффективнее, поскольку позволяет реализовать параллельные алгоритмы обработки информации, обеспечивающие одновременное разрешение многообразия проблем. Естественно, данный принцип должен востребоваться в нейросетевых моделях, правда, создание параллельных алгоритмов, как выясняется [20;26], представляет довольно сложную задачу. Кроме того, желательно, чтобы, как и в мозге, для нейросетевых моделей поддерживался достаточно высокий уровень надежности. По некоторым рекомендациям [20], вероятность правильного распознавания объектов для таких моделей должна быть близкой к 1 даже тогда, когда в сети отказывает до 50% элементов.

3). Универсальность и адаптивность сети.Как и мозг, сеть должна оптимально кодировать входной сигнал, реализуя универсальную обработку всевозможной внешней информации (зрительной, звуковой, обонятельной и т.п.). При этом следует предусмотреть возможность перенастройки сети с решения одного класса проблем на другой, тем самым, обеспечивая в необходимой мере адаптивность сети по отношению к внешнему информационному пространству.

4). Быстрый доступ к информации.Несмотря на крайне медленную (~100 м/с), по сравнению с компьютерами (~ 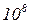м/с), скорость передачи сигналов и инерционность элементов мозга, его память работает весьма быстро. Скорее всего, мозг не рассматривает всю информацию, которой располагает, действуя гораздо рациональнее. На формальном языке это означает, что в сети следует предусмотреть оптимальные алгоритмы поиска кратчайших маршрутов между нейронами, выражающими искомый образ целевой функции. Формальное описание нейронной сети предусматривает следующие основные моменты:

1). Определение функциональных характеристик нейронов;

2). Задание общей архитектуры сети;

3). Указание правил взаимодействия между нейронами;

4). Описание алгоритма обучения сети, т.е. алгоритма формирования ассоциативных связей и их «развесовки» в соответствии с целями обучения.

Нейросеть должна адекватно реагировать на те образы, для распо-знавания которых она обучена. Например, если речь идет об учебном процессе, то в памяти нейросети должны содержаться образы (фрагменты) соответствующего программного (учебного) материала, а на вход этой сети поступают ответы обучаемого контингента по данному материалу, которые в процессе распознавания оцениваются или корректируются с помощью набора help-функций.

11.4. Нейросетевое обучение в дискретной модели Хопфилда/

Нейросеть как модель представляет собой динамическую систему 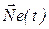в виде орграфа 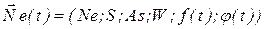, где Ne 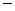конечный набор нейронов, представляющих вершины орграфа; S 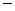множество состояний нейронов; As 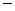набор ориентированных связей (дуг) между нейронами; W 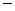веса связей. Состояние нейросети 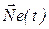на момент времени t определяется посредством функций: f(t): 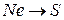, определяющей для каждого нейрона из Ne его состояние из S; и 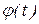: 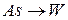, задающей каждой связи из As некоторый вес из множества W. Источники и стоки в нейросетях не фиксируются, т.е. формально любой элемент или их некоторый ансамбль в сети при необходимости может выполнять такие функции.

Модель Хопфилда [20;27;28] представляет собой следующую нейросетевую идеализацию. Полагается, что множество состояний 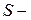дискретно, так, что S(t)={-1;1}, т.е. принимается два состояния активности нейронов – возбуждения (значение+1) и торможения (значение -1). Эта дискретность отражает нелинейный, пороговый характер функционирования нейрона и известный принцип нейробиологии «все или ничего» (см. п. 11.2).

Динамика нейрона у Хопфилда описывается в рамках традиционной модели нейрона Мак-Каллока – Питтса. Пусть 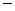некоторое состояние нейрона, а h(t) 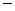внешнее воздействие на этот нейрон, например, со стороны других нейронов сети в момент времени t, которое считаем дискретным t=1;2;… . Тогда состояние данного нейрона в последующий момент времени s(t+1) определяется соотношением:

s(t+1)=sign(h(t))= 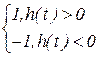(11.3)

В теории нейронных сетей считается, что всякая пара нейронов сети формально взаимосвязана. Поэтому, имея ввиду конечность множества нейронов Ne, пронумеровав элементы Ne, можно положить Ne={1;2;…;n}, где n – количество нейронов в сети, и тогда можно определить множество связей 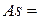{(i;j):i;j=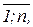 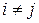} 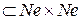. Будем также полагать, что воздействие на данный нейрон со стороны остальных нейронов сети отвечает принципу суперпозиции и определяется взвешенной суммой:

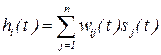, (11.4)

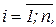
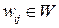
где 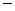вес дуги 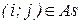, описывающей воздействие на нейрон i со стороны нейрона j в момент времени t. Таким образом, используя (11.3); (11.4), можно записать:

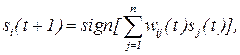
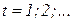(11.5)

Система нелинейных рекуррентных (разностных) уравнений 1-го порядка (11.5) описывает эволюцию нейросети 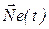, причем, входной образ

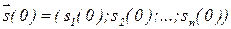, (11.6)

предъявляемый сети для распознания, определяет начальные условия для системы (11.5), а динамика изменения весов 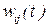представляет алгоритм обучения данной нейросети. В модели Хопфилда алгоритм обучения нейросети формируется в соответствии с правилом обучения, предложенным Д.Хеббом в 40-х гг. XX в. [20;23]. В данном случае, когда распознается единственный входной образ (11.6), правило Хебба принимает вид:

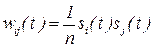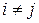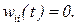, , (11.7)

Соотношения (11.5), (11.6), (11.7) полностью определяют эволюцию нейросети 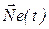в рамках нелинейной модели Хопфилда, причем, нелинейность этой модели связана с процедурой обучения (11.7).

Механизм обучения в нейросетевой модели Хопфилда (11.5), (11.6), (11.7) тесно связан с качественной теорией нелинейного дифференциального уравнения 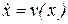где v(x) 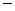некоторая ограниченная, достаточно гладкая функция скалярного аргумента x, обладающая потенциалом (функцией Ляпунова) L(x), т.е. 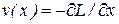. Известно [20], что аттракторами данного дифуравнения могут быть только особые точки 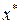, для которых 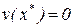, причем, на соответствующей фазовой координатной прямой устойчивые особые точки ( 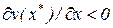) чередуются с неустойчивыми ( 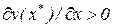) и последние определяют границы области притяжения устойчивых точек.

Сопоставим аттракторам рассматриваемого уравнения набор ключевых образов 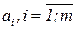, которым в сети отвечают вполне определенные устойчивые ассоциативные связи. Входной образ а, предъявляемый сети, задает начальное условие х(0) для этого уравнения; распознавание образа будет соответствовать выходу решения на аттрактор: предъявленный образ будет близок (в смысле (11.1)) к некоторому ключевому, если он попадает в область притяжения соответствующего аттрактора 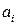и, следовательно, решение уравнения

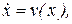
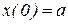(11.8)

при 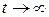стремится к одному из ключевых образов 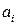, для которого 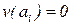. Таким образом, обучение сети в данном случае сводится к построению функции v(x) с устойчивыми особыми точками 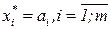, которым отвечают точки минимумов потенциала L(x).

Рассмотрим теперь разностную аппроксимацию уравнения (11.8) по методу Эйлера:

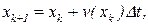
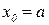(11.9)

Если 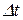достаточно мало, то свойства разностного уравнения (11.9), по крайней мере качественно, сохраняют свойства дифференциального уравнения (11.8) [20], а потому при 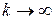решение уравнения (11.9) также выходит на некоторый аттрактор, отвечающий определенному ключевому образу и, таким образом, происходит распознавание входного образа 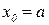, предъявленного сети.

Нетрудно заметить, что каждое уравнение системы (11.5) с условием (11.6) приводится к виду (11.9). Действительно, полагая 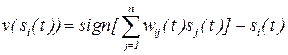, уравнение (11.5) принимает вид

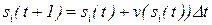, (11.10)

где 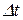=1, причем, единица временного шага 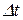должна устанавливаться на том уровне малости, который отвечает определенным условиям сходимости процесса (11.10) при 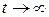. Сравнивая (11.10) и (11.9), убеждаемся, что эти уравнения отличаются только лишь некоторыми обозначениями и, следовательно, механизм обучения в дискретной нейросетевой модели Хопфилда (11.5), (11.6), (11.7) полностью укладывается в рамки сценария, описываемого качественной теорией уравнений (11.8), (11.9). Конкретным выражением процесса обучения в дискретной модели Хопфилда является тот факт, что после предъявления сети 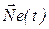входного образа (11.6) с ростом t происходит постепенная стабилизация весов связей (11.7) между нейронами. Как только отличия между соответствующими весами связи с ростом t перестают превосходить некоторые фиксированные значения (условие (11.1)), мы имеем режим выхода параметров сети на режим аттрактора, которому отвечает определенный ключевой образ и, таким образом, входной образ опознан, а соответствующая «развесованная» конфигурация связей между нейронами представляет результат обучения. Отметим, что обычно процедура стабилизации весов в процессе обучения нейросети оптимизируется по алгоритму обратного распространения ошибки [20].

11.5. «Нейросетевая педагогика» и ее приложения.

Как отмечалось (пп.11.1;11.2), в человеческом мозге путем самоорганизации нейронных ансамблей (гештальтов), формируются исключительно эффективные алгоритмы обучения, обеспечивающие необходимую коррекцию и самонастройку соответствующих программ. Поэтому цели нейродинамики – адекватно описать и воспроизвести эти алгоритмы на уровне абстрактных нейросетевых моделей, реализация которых в учебном процессе составляет предметную область «нейросетевой педагогики».

Одним из таких алгоритмов является нейросетевая модель обучения Хопфилда (п.11.4.), наглядно демонстрирующая, каким образом в принципе может быть организована память в сети, составленной из «не полностью надежных» элементов. Дидактически, в модели Хопфилда, по сути, реализуется хорошо известная процедура «натаскивания» субъекта на выполнение определенной деятельности. Отличаясь простотой и наглядностью, нейросеть Хопфилда, тем не менее сейчас является наиболее востребованной моделью и, например, дает адекватное описание таких практически важных объектов статистической физики, как спиновые стекла [20;29]. В целом, можно выделить три класса задач, реализуемых в рамках модели Хопфилда.

Классификация (распознавание образов).В этом случае, по заданному конечному набору признаков объекта, требуется классифицировать или идентифицировать данный объект [1]. Теоретические аспекты и некоторые приложения таких задач рассмотрены выше (пп.10.2;10.3), поэтому здесь обращается внимание на следующий важный момент. Поскольку нейросетевой подход реализует в себе одновременно быстродействие компьютера и способность мозга к обобщению и распознаванию, то нейросетевые модели оказываются особенно эффективными в задачах экспертной оценки. В работах [30-32] разработана математическая модель ЭС для реализации процедуры развивающего обучения в виртуальном образовательном пространстве. Наиболее трудоемким процессом при создании такой ЭС является формирование ее базы данных, которая выстраивается по экспертным оценкам и использование нейросетевой концепции обучения в этом случае оказывается очень эффективным.

В настоящее время нейросетевые модели широко используются в разных сферах [33]. С помощью нейросетевых моделей удается отслеживать и пресекать сомнительные операции с кредитными картами и банковскими чеками. На сегодняшний день система фирмы ITC, обеспечивающая безопасность кредитных карт Visa, в 1995 г. предотвратила нелегальные сделки на сумму более 100 млн. долл. Среди других областей приложения нейросетей можно указать медицинские диагностические ЭС, системы распознавания речи, оценки перспективности предприятий и др.

Кластеризация и поиск закономерностей.Кластерный анализ (или кластеризация) – это процедура упорядочивания объектов в сравнительно однородные классы на основе попарного сравнения этих объектов по предварительно определенным и измеренным критериям. При обучении в рамках данной процедуры обеспечивается реализация дидактических принципов системности и последовательности так, что, например, всякий учебник «кластеризован» по главам и, более мелко, по параграфам, которые тематически более-менее однородны и расположены в определенной последовательности: в физике раздел «Механика» содержит три кластера – статику, кинематику и динамику; школьный курс биологии состоит из ботаники, зоологии и физиологии человека; изучение русского языка включает фонетику, морфологию и синтаксис и т.д. Школьный учитель обычно проводит кластеризацию класса по успеваемости (отличники, хорошисты, троечники и двоечники). В экономике посредством кластерного анализа, например, удается эффективно выявлять фальсифицированные страховые случаи или маргинальные предприятия [33].

Факторный анализ (как поиск закономерностей) имеет своей задачей выделение факторов, которые интерпретируются как латентные причины взаимосвязи групп переменных, описывающих свойства изучаемого объекта. С помощью нейросети в рамках метода МГУА (метод группового учета аргументов), например, удается построить зависимость одного параметра от других в виде полинома. Вообще говоря, если в качестве элементов классификации выступают переменные, а в качестве мер их близости (или различия) – корреляции между ними, то, таким образом, фактически, происходит кластеризация свойств рассматриваемого объекта. В педагогике типичными примерами таких корреляций являются зависимости успеваемости от скорости чтения и скорости чтения по годам обучения школьников [34], кривая забывания Г. Эббингауза (1885, [35]) и др.

Прогнозирование.Задачей прогноза является построение научно-обоснованного суждения о возможных состояниях интересующего объекта в будущем, а также альтернативных путях и сроках их осуществления. В рамках нейросетевой модели прогноз сводится к анализу структур нейросети,которые возникают в рамках тех или иных гипотез о ее вероятном поведении в будущем, и выделению из этих конфигураций наиболее вероятной структуры, например, исходя из принципа минимизации энтропии системы.

Второй класс включает модели, отвечающие процессам, в которых будущее не зависит от прошлого, что равносильно отсутствию причинно-следственных связей между состояниями в таких процессах. Это класс стохастических моделей, к которому, например, относится система массового обслуживания. В образовании некоторое время считали, что, в силу неоднозначности хода педагогического процесса, описание сущности и связей педагогических явлений может строиться только в рамках теории вероятности [37;38].

В 70-х гг. XX в. обнаружился третий класс моделей, описывающих процессы в системах, эволюция которых обладает особенностями, например, бифуркацией. Развитие таких систем потенциально может иметь несколько сценариев и, какой из них конкретно реализуется, зависит от предыстории данного процесса, однако всегда является результатом малых воздействий в определенные моменты времени при определенных состояниях системы (в точках бифуркации). Иными словами, будущее в таких системах неоднозначно и зависит от более ранних состояний данной системы. Этот класс моделей отвечает эволюции открытой системы при ее взаимодействии с внешней средой и характерным для него является то обстоятельство, что у таких систем существуют принципиальные ограничения на временной период прогноза. Например, для прогноза погоды – это примерно две недели, а для динамики океана – около месяца. Есть основания полагать, что к данному классу относится большинство открытых систем, рассматриваемых в биосфере, экологии, теории цивилизаций, а также в госуправлении и, в частности, в образовании.

Имеющийся опыт показывает, что прогнозы в области образования, пока, в основном, строятся по экспертным оценкам, которые, как правило, скоррелированы со сценариями экономического развития государства [39;40]. Судя по всему, по экспертным оценкам построена «Национальная доктрина развития образования в РФ» (2000-2025 гг.) [41], в рамках которой прогнозируется сценарий развития российского образования на 25 лет. Впрочем, во время дискуссии при принятии данного государственного документа ректором МГУ им. М.В.Ломоносова В.А. Садовничим приводились доводы в пользу сокращения срока прогноза до 15 лет, однако они оказались в меньшинстве.