Модели распознавания образов на основе линейной алгебры.

Характерным примером процедуры распознавания образов является тестирование, при котором по ответам тестируемого устанавливается, насколько адекватно он представляет себе предложенный ему предметный контент. Во многих случаях эта процедура формируется на основе концепций линейной алгебры следующим образом [6].

Пусть I(m_k)=(x_1k;…; x_sk) – вектор-описание ответов x_ik, i= 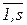объекта m_k, k= 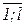в процедуре тестирования, в которой полагается x_ik 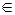{0;1}, где 0 – соответствует неверному, а 1 – верному ответам. Из векторов (x_1k;…; x_sk) формируется l-строчная матрица C_ls – ответов тестируемой аудитории. Выделяя в матрице ответов C_ls столбцы, в которых количество единиц (нулей) не превосходит некоторого нормативного значения, устанавливаются наиболее трудные (легкие) для данной аудитории задания и соответствующий контингент, который с ними справился. При этом, естественно, происходит разбиение тестовых заданий – на трудные, средней трудности и легкие, а тестируемой аудитории – на сильных, средних и слабых учащихся. Данная информация, с одной стороны, позволяет формировать базу данных, связанных с типизацией трудностей при изучении соответствующего предметного материала; с другой стороны, устанавли-вается тот контингент, с которым следует проводить специальные приемы обучения, как креативного, так и корректирующего характера.

Таким образом, анализ результатов тестирования с помощью матрицы C_ls позволяет оценить ряд важных параметров учебного процесса, связанных с тестируемой аудиторией, которые в этом случае представляют образы, распознаваемые в данном педагогическом измерении.