В социальной системе.
Формально, разбиение социометрической матрицы на «сильные» и «слабые» блоки сводится к определенной перенумерации строк (столбцов) матрицы, которая при этом переходит в некоторую матрицу 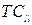 с выделенными блоками, после чего «сильным» блокам матрицы
с выделенными блоками, после чего «сильным» блокам матрицы 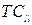 присваивается значение 1, а «слабым»
присваивается значение 1, а «слабым» 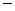 0 и, таким образом, реализуется отображение
0 и, таким образом, реализуется отображение 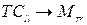 , где
, где 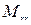
 соответствующая булева (
соответствующая булева (  )-матрица (
)-матрица ( 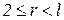 ), выражающая отношение симпатии в группе G.
), выражающая отношение симпатии в группе G.
Совершенно аналогично, путем опроса уровней антипатии, строится булева (  )-матрица
)-матрица  , выражающая отношение антипатии в учебной группе G. Матрицы
, выражающая отношение антипатии в учебной группе G. Матрицы 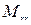 ;
; 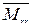 являются элементами конечной полугруппы
являются элементами конечной полугруппы 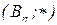
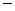 булевых (
булевых (  )-матриц, умножение
)-матриц, умножение 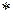 которых определяется по обычным правилам умножения матриц, рассматривая их элементы в рамках булевой алгебры. Интерпретируя матрицу
которых определяется по обычным правилам умножения матриц, рассматривая их элементы в рамках булевой алгебры. Интерпретируя матрицу 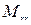 как отношение «друг», а
как отношение «друг», а 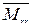 – как отношение «враг», в первую очередь, интерес представляют следующие произведения:
– как отношение «враг», в первую очередь, интерес представляют следующие произведения: 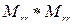 («друг друга»);
(«друг друга»); 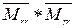 («враг врага»);
(«враг врага»); 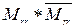 («друг врага») и
(«друг врага») и 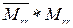 («враг друга»). Если использовать данные экспериментов [8], то по 2-му критерию разбиения (п.10.3.2) получается
(«враг друга»). Если использовать данные экспериментов [8], то по 2-му критерию разбиения (п.10.3.2) получается
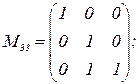
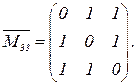
Непосредственно проверяется:
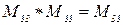 ;
; 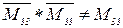 ;
; 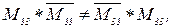
т.е., для данного сообщества, друг друга, скорее всего является твоим другом; враг врага не всегда является твоим другом, а друг врага не означает врага друга.
Подобная информация о социальной системе, в частности, учебной группе представляется важной и при обучении данную информацию можно эффективно реализовать по следующим каналам управления. Во-первых, следует задействовать данные по успеваемости, по которым группа разбивается на сильных, средних и слабых учащихся. Сравнивая эти данные с коалициями, которые выявлены в рамках опроса симпатий и антипатий в рассматриваемой группе, прежде всего, устанавливается, каким образом представлены сильные и слабые учащиеся в симпатизирующих коалициях, т.к. при этом проще наладить технологии сотрудничества между сильными и слабыми, что будет способствовать улучшению успеваемости в группе. Со слабыми учащимися, находящимися в антипатии к сильным, стратегия управления может строиться, как по линии организации дополнительных занятий по предмету, так и по пути сглаживания противоречий между сильными и слабыми учащимися. Во-вторых, приведенную полугрупповую конструкцию, выраженную матрицами 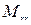 и
и 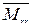 , можно развить путем введения представления о «ролевой структуре», как это предложено в работе [9]. Данное представление опирается на одну из теорем теории полугрупп [7], по которой всякое непустое подмножество полугруппы порождает в ней некоторую подполугруппу и ее, в социологическом контексте [9], определяют как ролевую структуру. В частности, в рассмотренном примере ролевая структура представляет собой 2-порожденную подполугруппу
, можно развить путем введения представления о «ролевой структуре», как это предложено в работе [9]. Данное представление опирается на одну из теорем теории полугрупп [7], по которой всякое непустое подмножество полугруппы порождает в ней некоторую подполугруппу и ее, в социологическом контексте [9], определяют как ролевую структуру. В частности, в рассмотренном примере ролевая структура представляет собой 2-порожденную подполугруппу 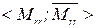
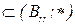 . Целесообразность рассмотрения ролевых структур обосновывается следующими соображениями. С одной стороны, по линии изоморфизма полугрупп удается устанавливать универсалии на многообразии сообществ, что позволяет выстраивать стандартные процедуры управления на классах универсальных ролевых структур. С другой стороны, таким образом удается сравнивать различные сообщества путем введения расстояния между ролевыми структурами [7].
. Целесообразность рассмотрения ролевых структур обосновывается следующими соображениями. С одной стороны, по линии изоморфизма полугрупп удается устанавливать универсалии на многообразии сообществ, что позволяет выстраивать стандартные процедуры управления на классах универсальных ролевых структур. С другой стороны, таким образом удается сравнивать различные сообщества путем введения расстояния между ролевыми структурами [7].
Лекция 11. Гештальт-психология и нейросетевые модели обучения.
Дата добавления: 2015-08-14; просмотров: 837;
