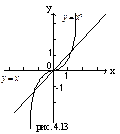Основные элементарные функции.
К основным элементарным функциям относятся:
1. степенные функции 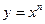 ,
, 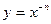 ,
, 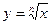 , где n – натуральное (
, где n – натуральное ( 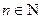 ).
).
2. показательные функции 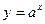 (
( 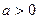 ,
, 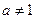 ).
).
3. логарифмические функции 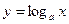 (
( 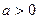 ,
, 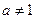 ).
).
4. тригонометрические функции 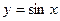 ,
, 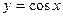 ,
, 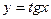 ,
, 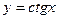 .
.
5. обратные тригонометрические функции 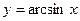 ,
, 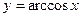 ,
, 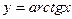 ,
, 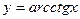 .
.
Понятие элементарной функции.Из основных функций новые функции могут быть получены двумя способами:
а) с помощью алгебраических действий;
б) с помощью операций образования сложной функции.
 Определение.Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Определение.Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Например, функция
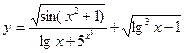
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции ( 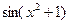 ,
, 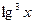 ,
, 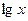 ,
, 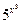 ,
, 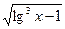 ) конечно.
) конечно.
Краткий обзор свойств основных элементарных функции представлен в таблице.
| Таблица | |||||||||
| Обозна-чение функции | Область опреде-ления Х | Область значе-ний Y | Четность, нечет-ность | Монотон-ность | Перио-дичность | Графики функций | |||
| 1. Степенная функция | |||||||||
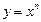
| (-∞;+∞)
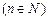
| (-∞;+∞), если n – нечетно [0;+∞), если n - четно | Нечетная, если n – нечетно; четная, если n – четно | Возрастает на (-∞;+∞), если n – нечетно; убывает на (-∞;0], если n – четно | 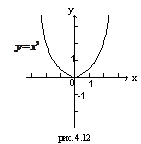 Неперио-дическая Неперио-дическая
|
| |||
| Продолжение таблицы | |||||||||
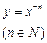
| (-∞;0)U U(0;+∞) | (-∞;0)U U(0;+∞)если n – нечетно [0;+∞), если n – четно | Нечетная, если n – нечетно; четная, если n – четно | Убывает на (-∞;0) и на (0;+∞), если n – нечетно; возрастает на (-∞;0) и убывает на (0;+∞), если n – четно | Неперио-дическая | 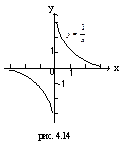
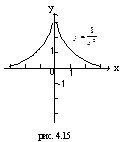
| |||
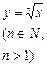
| (-∞;+∞) если n – нечетно [0;+∞) если n – четно | (-∞;+∞), если n – нечетно [0;+∞), если n - четно | Нечетная, если n – нечетно; общего вида, если n – четно | Возрастает на (-∞;+∞), если n – нечетно; возрастает на [0;+∞), если n – четно | Неперио-дическая | 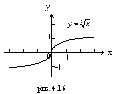

| |||
| 2. Показательная функция | |||||||||
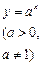
| (-∞;+∞) | (0;+∞) | общего вида | Возрастает на (-∞;+∞), если 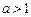 ; убывает на (-∞;+∞), если ; убывает на (-∞;+∞), если 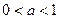
| Неперио-дическая | 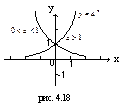
| |||
| 3. Логарифмическая функция | |||||||||
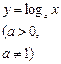
| (0;+∞) | (-∞;+∞) | общего вида | Возрастает на (0;+∞), если 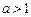 ; убывает на (0;+∞), если ; убывает на (0;+∞), если 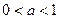
| Неперио-дическая |
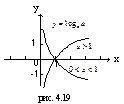
| |||
| Продолжение таблицы | |||||||||
| 4. Тригонометрические функции | |||||||||
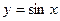
| (-∞;+∞) | [-1;1] | нечетная | Возрастает на [-π/2+2πn; π/2+2πn]; убывает на [π/2+2πn; 3π/2+2πn], 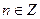
| Период 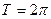
| 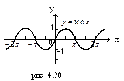
| |||
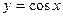
| (-∞;+∞) | [-1;1] | четная | Возрастает на [-π+2πn; 2πn]; убывает на [2πn; π+2πn], 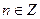
| Период 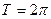
| 
| |||
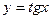
| (-π/2+ +πn;
π/2+πn);
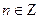
| (-∞;+∞) | нечетная | Возрастает на (-π/2+πn;
π/2+πn); 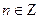
| Период 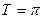
| 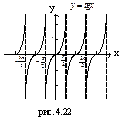
| |||
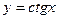
| (πn; π+πn);
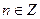
| (-∞;+∞) | нечетная | Убывает на (πn;π+πn);
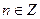
| Период 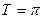
| 
| |||
| 5. Обратные тригонометрические функции | |||||||||
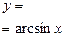
| [-1;1] | [-π/2; π/2] | нечетная | Возрастает на [-1;1] | Неперио-дическая | 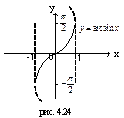
| |||
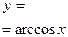
| [-1;1] | [0;π] | общего вида | Убывает на [-1;1] | Неперио-дическая | 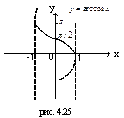
| |||
| Продолжение таблицы | |||||||||
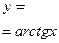
| (-∞;+∞) | (-π/2; π/2) | нечетная | Возрастает на (-∞;+∞) | Неперио-дическая | 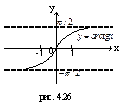
| |||
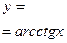
| (-∞;+∞) | (0;π) | общего вида | Убывает на (-∞;+∞) | Неперио-дическая | 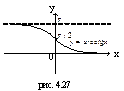
|
Классификация функций.
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраическойназывается функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:
• целая рациональная функция(многочленили полином):
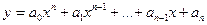 ;
;
• дробно-рациональная функция– отношение двух многочленов;
•иррациональная функция(если в составе операций над аргументом имеется извлечение корня).
Всякая не алгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся: показательная, логарифмическая, тригонометрические, обратные тригонометрические, гиперболические функции.
Дата добавления: 2015-08-14; просмотров: 1655;