Лекция 4. Функция. Основные определения.
Цель.Расширить понятие функции, известное студентам из школьного курса математики. Рассмотреть понятие области определения как множество точек числовой оси. Рассмотреть способы задания функции; понятие сложной функции. Рассмотреть линейную функцию.
Задачалекции – научиться находить область определения функции; строить прямую линию по заданному в различных формах условию; разбираться во взаимном расположении прямых на плоскости.
4.1. Числовые множества. Абсолютная величина числа, ее свойства.
4.2. Функция одной переменной. Способы задания.
4.3. Элементарные функции. Краткий обзор основных элементарных функций. Преобразования графиков.
4.4. Уравнение линии на плоскости. Линейная функция. Различные уравнения прямой линии.
4.1. Числовые множества. Абсолютная
величина числа и ее свойства.
В основе математики, как и любой науки, лежат первичные понятия, не определяемые через более простые понятия. К ним относятся: число, точка, множество.
Под множествомпонимается совокупность (набор) объектов, обладающих некоторым общим свойством. Эти объекты называются элементами или точками множества (множество студентов в данной аудитории, множество звезд на небе, множество букв в алфавите и так далее).
Множества обозначаются прописными буквами: A, B, X, Y, …, а их элементы соответствующими строчными буквами. Если элемент х принадлежит множеству Х, что записывают 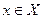 , или Х=(х1, х2,…, хn).
, или Х=(х1, х2,…, хn).
Если элемент у не принадлежит множеству Y, то записывается  . Если в множестве не содержится ни одного элемента, то оно называется пустым множеством и обозначается – Ø. Например, множество действительных корней уравнения
. Если в множестве не содержится ни одного элемента, то оно называется пустым множеством и обозначается – Ø. Например, множество действительных корней уравнения 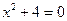 является пустым.
является пустым.
Если элементами множества являются числа, то оно называется числовым или точечным, так как всякое действительное число можно изобразить точкой на числовой оси (числовой прямой). Поэтому понятия «число х» и «точка х» можно считать эквивалентными.
Среди числовых множеств различают:
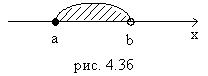
1. интервал (открытый отрезок) (а;b): это есть множество чисел, удовлетворяющих неравенству 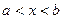 , (рис. 4.1)
, (рис. 4.1)
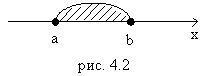
2. сегмент (закрытый отрезок) [a;b]: это множество чисел, удовлетворяющих неравенству 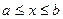 , (рис. 4.2)
, (рис. 4.2)
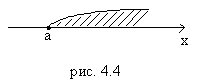
3. полуинтервалы 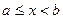 и
и 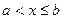 (рис. 4.3) среди этих множеств могут быть бесконечные, когда
(рис. 4.3) среди этих множеств могут быть бесконечные, когда 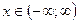 и полубесконечные: (-∞;a), (b;+∞), (-∞;a] и [b;+∞). Все указанные множества объединяются одним термином – промежутки Х.
и полубесконечные: (-∞;a), (b;+∞), (-∞;a] и [b;+∞). Все указанные множества объединяются одним термином – промежутки Х.


Следует различать такие понятия: объединение множеств, пересечение и разность множеств.
 Абсолютная величина числа и ее свойства.
Абсолютная величина числа и ее свойства.
Определение. Абсолютной величиной(или модулем) действительного числа х называется само число х, если оно неотрицательное, и противоположное число (-х), если оно отрицательное:
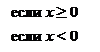
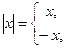
Из определения очевидно, что  .
.
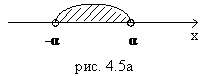 Рассмотрим некоторые свойства модуля.
Рассмотрим некоторые свойства модуля.
1. Если 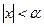 , то
, то 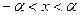 (рис. 4.5)
(рис. 4.5)
а) 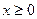 , тогда
, тогда 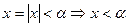
б) 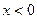 , тогда
, тогда 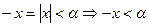 и
и 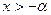
откуда следует неравенство 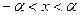
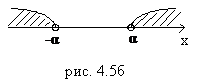 Из сказанного автоматически вытекает:
Из сказанного автоматически вытекает:
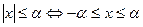 и
и
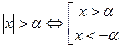
2. Если 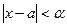 , то
, то 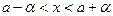 , то есть
, то есть 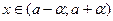 . Абсолютная величина разности
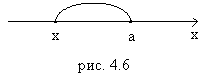
. Абсолютная величина разности  характеризует расстояние от точки х до точки а, независимо от того, находится ли точка х левее или правее точки а (рис. 4.6)
характеризует расстояние от точки х до точки а, независимо от того, находится ли точка х левее или правее точки а (рис. 4.6)
Всякий интервал, содержащий точку а, называется окрестностью точки а.
Интервал 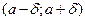 , то есть множество точек, удовлетворяющих неравенству
, то есть множество точек, удовлетворяющих неравенству  , где
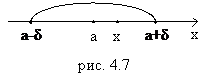
, где 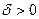 (см. п.2), называется δ-окрестностью точки а (рис. 4.7).
(см. п.2), называется δ-окрестностью точки а (рис. 4.7).
 |
Можно сказать, что δ-окрестность представляет собой множество точек х, расстояние от каждой из которых до точки 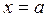 меньше δ.
меньше δ.
3. Модуль суммы 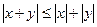 .
.
Доказательство:
а) пусть 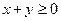 , тогда
, тогда 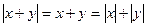 ;
;
б) пусть 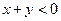 , в этом случае
, в этом случае 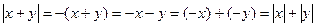 ;
;
Можно доказать, что модуль разности  , модуль произведения
, модуль произведения  , модуль частного
, модуль частного 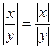 , если
, если 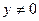 .
.
4.2. Понятие функции. Основные свойства функций.
Постоянной величинойназывается величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру – число π.
Переменнойназывается величина, которая может принимать различные числовые значения. Например, при равномерном движении 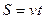 , где путь S и время t – переменные, или площадь треугольника
, где путь S и время t – переменные, или площадь треугольника 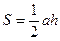 , где S – площадь, h – высота, a – постоянное основание.
, где S – площадь, h – высота, a – постоянное основание.
Перейдем к понятию функции.

Определение.Если каждому значению x множества Х 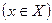 ставится в соответствие вполне определенное значение у множества Y
ставится в соответствие вполне определенное значение у множества Y 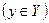 , то говорят, что на множестве Х задана функция
, то говорят, что на множестве Х задана функция 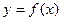 .
.
При этом х называется независимой переменной, или аргументом, у – зависимой переменной, а буква f обозначает закон соответствия.
Множество Х называется областью определения, или существования, функции, а множество Y – областью значений функции.
Под символом 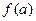 понимается значение функции при
понимается значение функции при 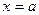 . Можно записать в виде
. Можно записать в виде 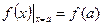 . Если
. Если  области определения, то символ
области определения, то символ 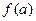 не имеет смысла.
не имеет смысла.
Примеры. Найти область определения функций:
1. 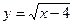 , область определения Х:
, область определения Х: 
2. 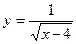 , область определения Х:
, область определения Х: 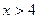
3. 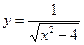 , область определения – множество чисел, удовлетворяющих условию
, область определения – множество чисел, удовлетворяющих условию  , или
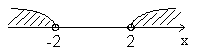
, или 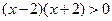 . На числовой оси это есть точки (числа), удовлетворяющие условию
. На числовой оси это есть точки (числа), удовлетворяющие условию 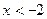 и
и 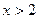 .
.
Дата добавления: 2015-08-14; просмотров: 827;
