Производная по направлению. В математическом анализе, производная по направлению – это обобщение понятия производной на случай функции многих переменных

В математическом анализе, производная по направлению – это обобщение понятия производной на случай функции многих переменных. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Производная скалярного поля 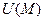по направлению ℓ, заданному вектором 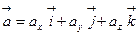, вычисляется по формуле , где

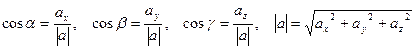
Абсолютное значение производной о направлению определяет скорость изменения скалярного поля в точке М, а её знак – характер изменения (возрастания или убывания).

Пример 2. Найти производную от функции 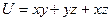в точке 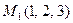в направлении, идущем от этой точки к точке .

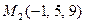Решение:

syms x y z

>> U=x*y+y*z+x*z;

>> M1=[1 2 3];

>> M2=[-1 5 9];

>> dudxM1=subs(diff(U,x),[x,y,z],M1) %частные производные функции в точке

dudxM1 = 5

>> dudyM1=subs(diff(U,y),[x,y,z],M1)

dudyM1 = 4

>> dudzM1=subs(diff(U,z),[x,y,z],M1)

dudzM1 = 3

>> M2M1=M2-M1

M2M1 = -2 3 6

>> L=M2M1/norm(M2M1) % направляющие косинусы

L = -0.2857 0.4286 0.8571

>> dudl=dudxM1*L(1,1)+dudyM1*L(1,2)+dudzM1*L(1,3)

dudl =. 20/7