Градиент.

Пусть в области V дано скалярное поле

Определение: Градиентом дифференцируемой функции 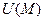) называется вектор 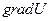, направленный по нормали к поверхности уровня поля в сторону возрастания поля, компоненты которого являются частными производными функции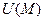

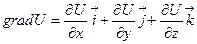
Градиент (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».

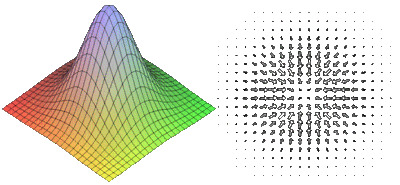
Таким образом операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что вектора направлены в горку и тем длиннее, чем круче наклон.

Основные свойства градиента

1. 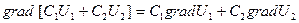, 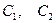- произвольные постоянные.

2. .

3. .

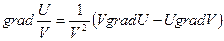4.

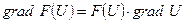
Вектор, противоположный градиенту - 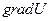называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю. На свойствах градиента основаны методы первого порядка, называемые также градиентным и методами минимизации. Использование этих методов в общем случае позволяет определить точку локального минимума функции.

Длина градиента равна наибольшей скорости изменения поля 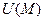в точке М.