Инерциальная система геометрического типа.

У таких ИНС первый базовый триэдр совмещается с горизонтальной системой коордтнат, а вторая – не вращается относительно инерциального пространства.

ИНС геометрического типа характеризуется следующими условиями:

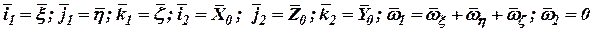
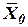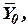
где , 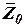- орты инерциальной системы координат .

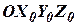За инерциальную систему координат чаще всего принимают экваториальную систему координат.

В качестве примера рассмотрим схему ИНС с вращающейся системой координат (рис. 2).

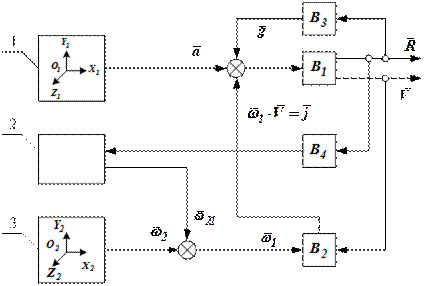
Рисунок 2 Функциональная схема ИНС с вращающейся системой координат

1 – блок акселерометров; 2 – ГСП; 3 – блок датчиков угловой ориентации;

… - вычислительные устройства.

Принцип построения данной ИНС основан на использовании акселерометров и датчиков угловой ориентации. Блок акселерометров 1 измеряет вектор ускорения 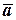; гиростабилизированная платформа 2 осуществляет кинематическую связь акселерометров с датчиками угловой ориентации 3. Кинематическая связь между первым 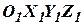и вторым 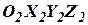базовыми триэдрами определяется при помощи матрицы направляющих косинусов 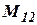. Вычислитель 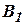является основным навигационным вычислителем. Его задача заключается в выработке текущей информации о координатах центра масс ЛА ( ) и вектора скорости ( ). 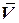Вычислитель 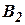предназначен для вычисления кориолисового ускорения 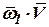; 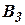- вычислитель вектора гравитационного ускорения 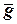; 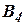- вычислитель управляющих сигналов системы угловой стабилизации акселерометров.

Инерциальная навигационная система может быть построена только на датчиках линейных ускорений (акселерометрах). Для реализации таких ИНС может быть использовано шесть, девять и более однокомпонентных акселерометров, имеющих различные ориентации осей чувствительности.

Если гравитационное ускорение задается или вычисляется в специальном вычислителе, то для построения ИНС достаточно шести акселерометров. Пусть оси чувствительности акселерометров 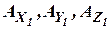образуют первый базовый триэдр 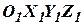, а оси чувствительности акселерометров 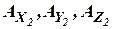- соответственно второй базовый триэдр 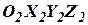. Расположим акселерометры на общем жестком основании 1. Расстояние между полюсами триэдров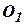 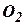обозначим через 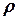. В общем 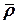- это радиус-вектор, соединяющий точк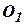и и 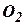. Одноименные оси триэдров расположим параллельно ( ; ; ).

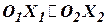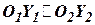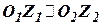Функциональная схема ИНС на базе шести акселерометров приведена на рис. 3.

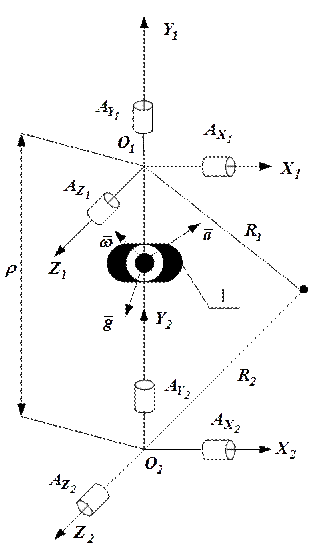
Рисунок 3 ИНС на основе шести акселерометров

1 – жесткое основание; 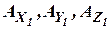, 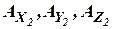- акселерометры.

На основании сигналов акселерометров получим следующие навигационные уравнения:

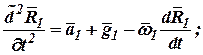
(10)

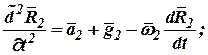
(11)

;

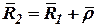(12)

.

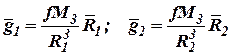(13)

.

Таким образом, два векторных уравнения (10) и (11) содержат две неизвестные величины 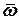и 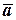. Совместное решение уравнений (10)…(13), с учетом заданного вектора 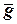, позволяет полностью решить навигационную задачу.