НАВИГАЦИОННЫХ СИСТЕМ
В общем случае при построении инерциальных систем необходимо учитывать следующее:
· способы измерения навигационных параметров ЛА относительно навигационной системы отсчета 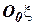
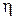
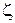 ;
;
· виды ориентации акселерометров;
· особенности моделирования систем координат;
· методы учета гравитационного ускорения;
· методы учета начальных параметров движения.
В связи с этим в состав любой инерциальной системы входят следующие функциональные элементы:
· система акселерометров, измеряющая составляющие вектора 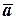 ускорения движения центра масс ЛА под действием активных сил;
ускорения движения центра масс ЛА под действием активных сил;
· датчики угловой ориентации, моделирующие навигационную систему координат или измеряющие ее угловую скорость вращения;
· датчики первичной и исходной информации, в том числе и данных о гравитационном поле;
· счетно-решающее устройства для вычисления навигационных алгоритмов;
· системы отображения выходной информации или выдачи выходных сигналов различным потребителям;
· системы управления и коррекции погрешностей.
Введем в рассмотрение два базовых ортогональных триэдра:
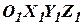 - первый базовый триэдр, образованный осями чувствительности акселерометров;
- первый базовый триэдр, образованный осями чувствительности акселерометров;
 - второй базовый триэдр, совпадающий с осями чувствительности датчиков угловой ориентации (моделирует навигационную системы координат).
- второй базовый триэдр, совпадающий с осями чувствительности датчиков угловой ориентации (моделирует навигационную системы координат).
Триэдр 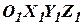 вращается с абсолютной угловой скоростью
вращается с абсолютной угловой скоростью 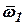 относительно инерциальной системы отсчета
относительно инерциальной системы отсчета 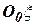
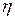
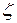 .
.
Вектор измеренного ускорения в системе координат 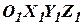 равен
равен
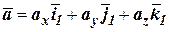 , ,
| (1) |
где 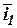 ,
, 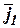 ,
, 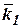 - орты системы координат
- орты системы координат 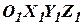 .
.
Запишем навигационное уравнение, учитывающее абсолютное ускорение центра масс ЛА, в виде
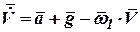 , ,
| (2) |
где 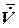 - производная по времени от вектора скорости в системе координат
- производная по времени от вектора скорости в системе координат 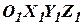 , вращающийся с угловой скоростью
, вращающийся с угловой скоростью 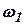 .
.
В уравнении (2) компоненты ускорения 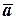 измеряются акселерометрами, гравитационное ускорение задается одним из каких-либо способов, скорость
измеряются акселерометрами, гравитационное ускорение задается одним из каких-либо способов, скорость 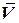 получают из выхода интеграторов ускорения,
получают из выхода интеграторов ускорения, 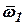 получают от датчиков угловых скоростей или датчиков угловой ориентации.
получают от датчиков угловых скоростей или датчиков угловой ориентации.
Положение акселерометров относительно датчиков угловой ориентации имеет следующие особенности. Если связь между акселерометрами и датчиками угловой ориентации жесткая, то первый 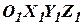 и второй
и второй  базовые триэдры совпадают. С помощью кардановых рамок связь между акселерометрами и датчиками угловой ориентации ЛА может быть гибкой. В этом случае триэдры
базовые триэдры совпадают. С помощью кардановых рамок связь между акселерометрами и датчиками угловой ориентации ЛА может быть гибкой. В этом случае триэдры 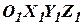 и
и  могут быть повернуты относительно друг друга на некоторые углы. Значение величин этих углов, естественно, должны быть известными. Тогда переход от первого базового триэдра ко второму можно осуществлять на основании известных матриц направляющих косинусов,
могут быть повернуты относительно друг друга на некоторые углы. Значение величин этих углов, естественно, должны быть известными. Тогда переход от первого базового триэдра ко второму можно осуществлять на основании известных матриц направляющих косинусов,
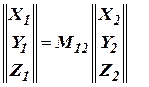 и и 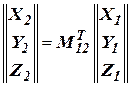 , ,
| (3) |
где 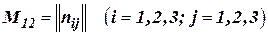 ;
;
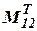 - транспонированная матрица от матрицы
- транспонированная матрица от матрицы 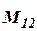 .
.
Второй базовый триэдр  может вращаться относительно инерциальной пространства с угловой скоростью
может вращаться относительно инерциальной пространства с угловой скоростью 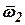 . Скорость
. Скорость 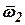 задается или измеряется:
задается или измеряется:
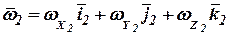 , ,
| (4) |
где 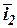 ,
, 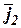 ,
, 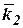 - орты системы координат
- орты системы координат  .
.
Для решения навигационной задачи в соответствии с уравнением (2) необходимо определить вектор угловой скорости 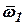 , равный
, равный
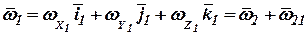 , ,
| (5) |
где 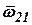 - вектор угловой скорости триэдров
- вектор угловой скорости триэдров 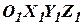 и
и  относительно друг друга.
относительно друг друга.
Тогда навигационное уравнение (2) с учетом (5) принимает вид:
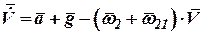 . .
| (6) |
Исходя из выражения (6), можно выделить следующие характерные особенности и условия построения различного типа инерциальных систем навигации.
Дата добавления: 2015-08-14; просмотров: 1117;
