ИСПОЛЬЗУЮЩИЕ ПРОИЗВОДНЫЕ ФУНКЦИИ

Будем рассматривать задачу безусловной оптимизации (4.1) предполагая, что функция 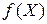непрерывно дифференцируема на 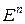. Для ее решения воспользуемся простейшими итерационными процедурами вида

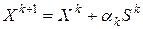, (6.1)

где направление убывания 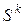будем определять тем или иным способом с использованием информации о частных производных функции 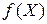в точке 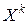. Если 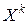не является стационарной точкой, т.е. 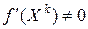, то в этой точке существует бесконечное множество направлений убывания. Какому из них отдать предпочтение? Будем рассуждать так.

Согласно определению (4.2) дифференцируемой функции её приращение в точке 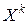выражается так

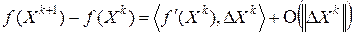(6.2)

Если 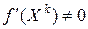, то при достаточно малых 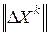главная часть приращения (6.2) будет определяться дифференциалом функции 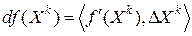. С учетом неравенства Коши - Буняковского справедливо соотношение

,

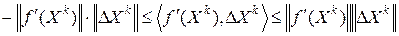причем, если 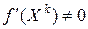, то правое неравенство обращается в равенство только при 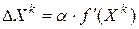, а левое неравенство – только при 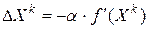, где 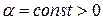. Отсюда ясно, что при 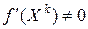направление наибыстрейшего возрастания функции 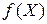в точке 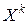совпадает с направлением градиента 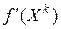, а направление наибыстрейшего убывания с направлением антиградиента .

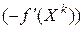Это свойство градиента и кладется в основу так называемых градиентных методов минимизации функции. Таким образом, при решении задачи (4.1) с помощью итерационной процедуры (6.1) в качестве направления убывания целесообразно выбирать направление антиградиента. Как и все итерационные методы, они предполагают выбор начального приближения – некоторой точки 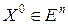. Общих правил этого выбора нет. В тех случаях, когда известна какая-либо априорная информация об области расположения точки минимума, начальное приближение 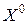выбирают поближе к этой области.

Пусть начальная точка 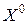уже выбрана. Тогда градиентный метод заключается в построении последовательности точек 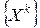по правилу

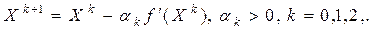(6.3)

Число 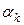из (6.3) называют длиной шага или просто шагом градиентного метода. Если 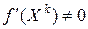, то шаг 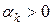можно выбрать так, чтобы 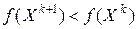. В самом деле, из равенства (6.2) имеем

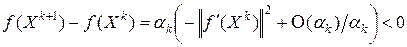
при всех достаточно малых 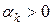. Если 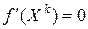, то 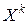- стационарная точка. В этом случае процесс (6.3) прекращается и, при необходимости, проводится дополнительное исследование поведения функции в окрестности точки 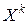для выяснения того, достигается ли в этой точке 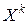минимум функции 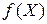или не достигается. В частности, если 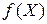- выпуклая функция, то в стационарной точке всегда достигается минимум.

Существуют различные способы выбора величины 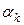в методе (6.3). В зависимости от способа выбора 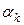можно получить различные варианты градиентного метода. Далее рассмотрим из них наиболее употребительные на практике.