Метод градиентного спуска
В соответствии с основной идеей градиентного метода минимизирующая последовательность 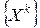 строится по правилу (6.3), т.е. в качестве направления убывания функции
строится по правилу (6.3), т.е. в качестве направления убывания функции 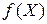 выбирается направление антиградиента (
выбирается направление антиградиента ( 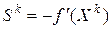 ), которое, как показано выше, обеспечивает в малой окрестности точки
), которое, как показано выше, обеспечивает в малой окрестности точки 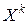 наискорейшее убывание функции
наискорейшее убывание функции 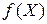 . В качестве длины шага
. В качестве длины шага 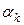 в этом варианте градиентного метода находится какое-либо число
в этом варианте градиентного метода находится какое-либо число 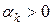 , обеспечивающее условие монотонного убывания функции
, обеспечивающее условие монотонного убывания функции
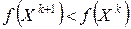 . (6.4)
. (6.4)
С этой целью задается какое-либо число 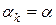 . При этом для каждого
. При этом для каждого 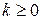 проверяют условие монотонного убывания (6.4), и в случае его нарушения величину
проверяют условие монотонного убывания (6.4), и в случае его нарушения величину 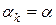 дробят до тех пор, пока не восстановится монотонность метода.
дробят до тех пор, пока не восстановится монотонность метода.
Приведем алгоритм одного из вариантов метода градиентного спуска.
Шаг 0. Задать параметр точности 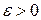 , начальный шаг
, начальный шаг 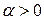 , параметр алгоритма
, параметр алгоритма 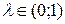 , выбрать
, выбрать 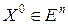 , вычислить значение
, вычислить значение 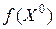 , положить
, положить 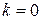 .
.
Шаг 1. Найти градиент 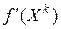 и проверить условие достижения заданной точности
и проверить условие достижения заданной точности 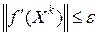 . Если оно выполняется, то перейти к шагу 6, иначе - к шагу 2.
. Если оно выполняется, то перейти к шагу 6, иначе - к шагу 2.
Шаг 2. Найти новую точку 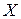 в направлении антиградиента
в направлении антиградиента 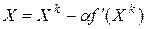 и вычислить
и вычислить 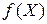 .
.
Шаг 3. Проверить неравенство
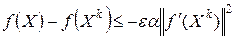 , (6.5)
, (6.5)
где 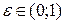 - произвольно выбранная константа, одинаковая для всех итераций.
- произвольно выбранная константа, одинаковая для всех итераций.
Шаг 4. Если неравенство (6.5) выполняется, то положить  ,
, 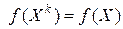 ,
, 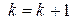 и перейти к шагу 1, иначе - перейти к шагу 3.
и перейти к шагу 1, иначе - перейти к шагу 3.
Шаг 5. Положить 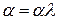 , где
, где 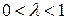 и перейти к шагу 2.
и перейти к шагу 2.
Шаг 6. Завершить вычисления, положив 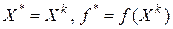 .
.
Замечание. Вблизи стационарной точки функции 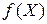 величина
величина  становится малой. Это может привести к замедлению сходимости последовательности
становится малой. Это может привести к замедлению сходимости последовательности 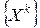 . Поэтому в (6.3) вместо вектора антиградиента
. Поэтому в (6.3) вместо вектора антиградиента 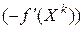 используют вектор единичной длины
используют вектор единичной длины 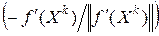 .
.
Обоснуем сходимость описанной итерационной процедуры, доказав возможность выбора длины шага 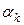 , обеспечивающего сходимость последовательности
, обеспечивающего сходимость последовательности 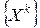 к стационарной точке. Для этого на функцию
к стационарной точке. Для этого на функцию 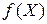 кроме условия непрерывной дифференцируемости, приходится накладывать дополнительные более жесткие условия.
кроме условия непрерывной дифференцируемости, приходится накладывать дополнительные более жесткие условия.
Теорема 6.1. Если функция 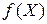 ограничена снизу, ее градиент
ограничена снизу, ее градиент 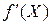 удовлетворяет условию Липшица, т.е.
удовлетворяет условию Липшица, т.е.
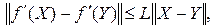 (6.6)
(6.6)
с конечной константой 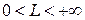 при любых
при любых 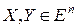 , а выбор
, а выбор 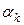 производится описанным способом, то для процесса (6.3) норма градиента
производится описанным способом, то для процесса (6.3) норма градиента 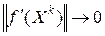 при
при 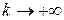 , какова бы ни была начальная точка
, какова бы ни была начальная точка 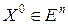 .
.
Д о к а з а т е л ь с т в о. По теореме о среднем
 ,
,
где 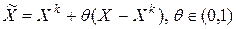 . Тогда учитывая, что в рассматриваемой итерационной процедуре
. Тогда учитывая, что в рассматриваемой итерационной процедуре 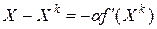 имеем
имеем
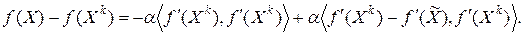
В силу неравенства Коши-Буняковского
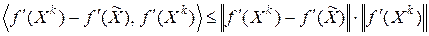
и условия Липшица (6.6) имеют место неравенства
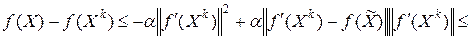
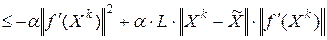 .
.
Учитывая, что 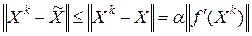 , получаем
, получаем
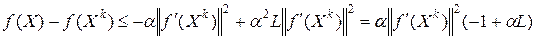 .
.
Из полученного соотношения видно, что существуют 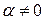 , при которых неравенство (6.5) справедливо. Для этого достаточно выбрать значение параметра
, при которых неравенство (6.5) справедливо. Для этого достаточно выбрать значение параметра 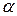 , удовлетворяющее условию
, удовлетворяющее условию 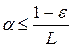 . Поскольку
. Поскольку 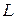 - ограниченная величина, а
- ограниченная величина, а 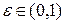 , то всегда можно это сделать.
, то всегда можно это сделать.
Таким образом, если выбирать 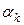 по указанному способу, то
по указанному способу, то
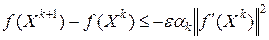 . (6.7)
. (6.7)
Отсюда с учетом того, что правило выбора 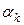 при любом
при любом 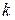 гарантирует
гарантирует 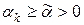 (в качестве
(в качестве 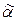 можно взять любую константу, не превосходящую
можно взять любую константу, не превосходящую 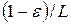 )), следует, что
)), следует, что 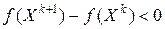 при любом
при любом 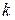 , если
, если 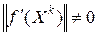 и что
и что
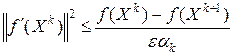 . (6.8)
. (6.8)
Далее поскольку функция ограниченна снизу и 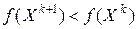 при любом
при любом 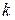 , то при
, то при 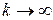
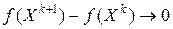 (6.9)
(6.9)
Тогда из (6.8), (6.9) вытекает, что 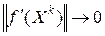 при
при 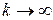 .
.
Дата добавления: 2015-08-14; просмотров: 704;
