Исследование устойчивости по линейному приближению.
В некоторых случаях устойчивость состояния равновесия нелинейной системы можно исследовать по уравнениям первого приближения, полученным в результате линеаризации уравнений состояния в малой окрестности точки равновесия. Данный способ был предложен A.M. Ляпуновым.
Рассмотрим этот подход для нелинейной автономной стационарной системы
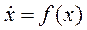 ,
, 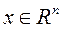 ,
, 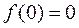 . (7)
. (7)
Разложим f(x) в ряд Тейлора в малой окрестности состояния равновесия:
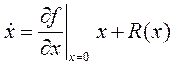 , (8)
, (8)
где R(x) - члены ряда разложения выше первой степени; матрица частных производных 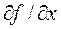 имеет вид
имеет вид

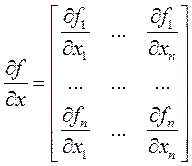 . (9)
. (9)
Отбрасывая члены ряда разложения R(x), вместо (8) получим
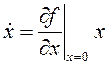 . (10)
. (10)
Матрица частных производных (9) рассматривается в точке равновесия, поэтому представляет собой числовую матрицу коэффициентов (якобиан), для которой введем обозначение
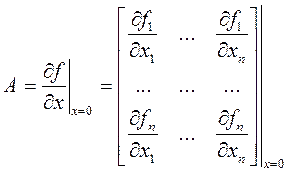 . (11)
. (11)
С учетом (11) окончательно уравнение первого приближения системы (10) принимает вид
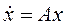 , (12),
, (12),
т. е. соответствует описанию линейной автономной системы.
Согласно теореме, доказанной A.M. Ляпуновым, устойчивость исходной системы (7) связана с устойчивостью линеаризованной системы (12).
Теорема.
· Если линеаризованная система устойчива, то исходная нелинейная система будет асимптотически устойчивой «в малом» относительно исследуемого состояния равновесия.
· При неустойчивой линеаризованной системе процессы в исходной нелинейной системе будут также неустойчивыми.
· Если линеаризованная система находится на границе устойчивости (корни нулевые или мнимые), то об устойчивости нелинейной системы ничего нельзя сказать. Это критический случай, и нужны дополнительные исследования для окончательного суждения об устойчивости нелинейной системы (7), которую определяют члены высшего порядка ряда разложения R(x).
Пример 1.
По линейному приближению оценить устойчивость относительно одного из положений равновесия системы, математическая модель которой имеет вид
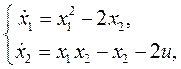 u=0.
u=0.
Запишем уравнения равновесия системы
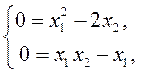
откуда определим одну из точек равновесия: 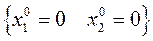 . В ее малой окрестности линеаризуем исходную систему
. В ее малой окрестности линеаризуем исходную систему
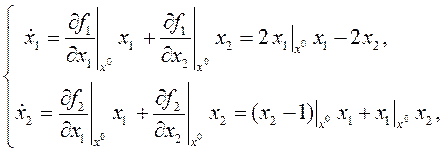
которая примет вид
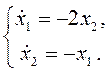
Матрица линеаризованной системы следующая:
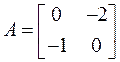 .
.
Запишем для нее характеристическое уравнение
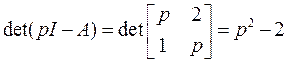 .
.
Как видим, линеаризованная система неустойчива, следовательно, исходная система также неустойчива.
Дата добавления: 2015-08-14; просмотров: 1332;
