Понятие об устойчивости состояния равновесия.

Поскольку поведение нелинейной системы существенно зависит от величины внешних воздействий, их численное значение всегда оговаривается при анализе ее свойств. Исследуем понятие устойчивости состояния равновесия для автономной стационарной системы, уравнение состояния которой имеет вид

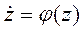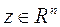, . (1)

Обычно нас интересует устойчивость относительно состояния равновесия 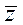=const, так что

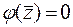. (1a)

Задачу анализа можно свести к проверке устойчивости системы относительно начала координат в пространстве новых переменных (относительно нулевого состояния равновесия).

С этой целью введем вектор переменных x, в качестве которых выберем отклонение от состояния равновесия

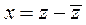. (2)

Дифференцируя (2) по времени, получим уравнение состояния для новых переменных

,

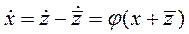которое запишем в виде

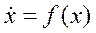. (3)

В пространстве состояний x согласно (1a), (2) и (3) точка (состояние) равновесия совпадает с началом координат, т. е.

. (4)

Рассмотрим теперь условия устойчивости автономной системы (3) относительно точки х=0 (нулевого состояния равновесия).

Состояние равновесия системы называется асимптотически устойчивым, если при движении из начального состояния выполняется условие

, .

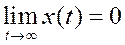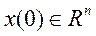Условие (5) означает, что с течением времени фазовые траектории системы «стягиваются» к началу координат (рис. 1). При неустойчивом движении фазовая траектория удаляется от точки равновесия или вырождается в предельный цикл.

В зависимости от значений x(0), для которых выполняется условие (5), различают устойчивость «в малом» и «в большом».

Состояние равновесия системы называется асимптотически устойчивым «в малом», если это свойство выполняется для малой окрестности положения равновесия (локальная устойчивость).

Состояние равновесия системы называется асимптотически устойчивым «в большом», если условие (5) выполняется для любых начальных условий из рабочей области пространства состояний (глобальная устойчивость).

Состояние равновесия системы называется экспоненциально устойчивым, если оно устойчиво асимптотически и выполняется условие

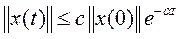, (6)

где с = const>0, а = const>0.

В зависимости от начальных условий также можно выделить экспоненциальную устойчивость «в малом» и «в большом».

Отметим, что для систем автоматики важно наличие именно экспоненциальной устойчивости, которая гарантирует и скорость затухания переходных процессов (с показателем а). Свойства асимптотической устойчивости недостаточно для работы реальных систем.