Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны.

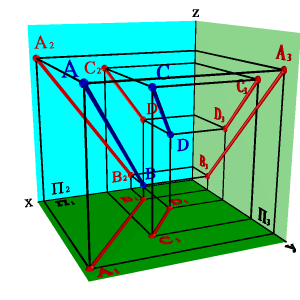
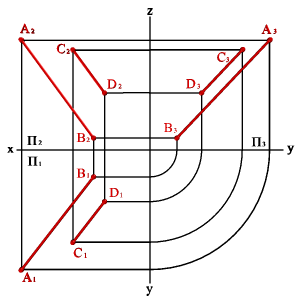
Это свойство параллельного проецирования остается справедливым и для ортогональных проекций, то есть если ABCD то A₁B₁C₁D₁; A₂B₂C₂D₂; A₃B₃C₃D₃(рис.3.19). В общем случае справедливо и обратное утверждение.

а) модель		б) эпюр
Рисунок 3.19. Параллельные прямые

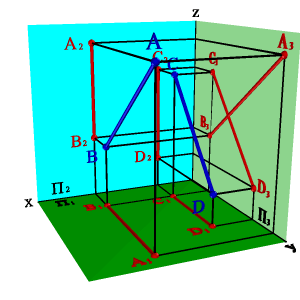
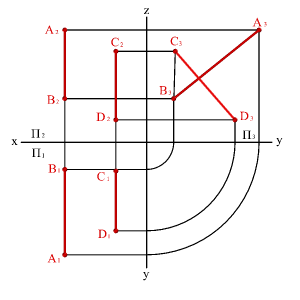
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 3.20). В рассмотренном случае проекции отрезков на плоскость П₃ пересекаются, следовательно, они не параллельны.

Решение этого вопроса можно получить сравнением двух соотношений если:

А₂В₂/ А₁В₁= С₂Д₂/ С₁ Д₁Þ АВ//СД

А₂В₂/ А₁В₁¹ С₂Д₂/ С₁Д₁Þ АВ#СД

а) модель		б) эпюр
Рисунок 3.20. Прямые параллельные профильной плоскости проекций