Лекция 7. § 141. Теорема о том, что всякое уравнение второй степени с двумя неизвестными определяет эллипс, гиперболу, параболу или две прямые линии.
Аналитическая геометрия.
Глава 11. Линии второго порядка, заданные общими уравнениями
Лекция 7. § 141. Теорема о том, что всякое уравнение второй степени с двумя неизвестными определяет эллипс, гиперболу, параболу или две прямые линии.
Общее уравнение линии второго порядка записывается в следующем виде:
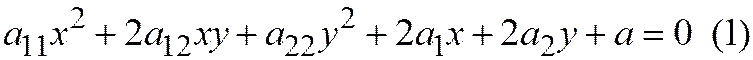
Все коэффициенты обозначены одной буквой 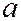 с индексами, указывающими, какая координата в какой степени умножается на этот коэффициент (
с индексами, указывающими, какая координата в какой степени умножается на этот коэффициент ( 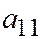 -коэффициент при
-коэффициент при  и т.д.). Через
и т.д.). Через 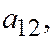
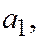
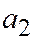 обозначены, соответственно, половины коэффициентов перед
обозначены, соответственно, половины коэффициентов перед 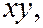
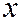 и
и 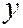 для симметрии последующих формул. Все коэффициенты считаются действительными числами.
для симметрии последующих формул. Все коэффициенты считаются действительными числами.
Теорема 1. Общее уравнение линии второго порядка 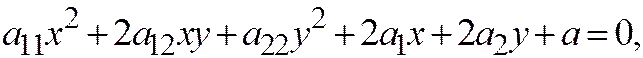
заданной относительно Декартовой прямоугольной системы координат, при помощи поворота и переноса осей координат можно привести к одному из следующих видов:
I. 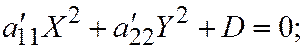 где
где 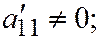
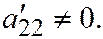 II.
II. 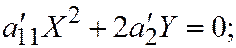 где
где 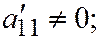
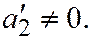
III. 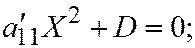 где
где 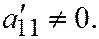
Эти уравнения называются простейшими уравнениями линии второго порядка.
Доказательство. Докажем сначала, что можно повернуть оси  на такой угол
на такой угол  , что в преобразованном уравнении коэффициент при произведении новых координат
, что в преобразованном уравнении коэффициент при произведении новых координат 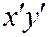 обратится в нуль.
обратится в нуль.
Итак, предполагая, что 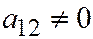 , повернём оси
, повернём оси 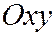 пока на произвольный угол
пока на произвольный угол 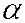 . Тогда координаты
. Тогда координаты 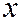 и
и 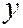 точки
точки 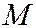 в системе
в системе 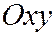 через координаты
через координаты 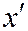 и
и 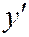 той же точки
той же точки 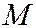 в системе
в системе 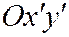 будут
будут
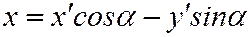 ,
,
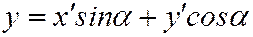 .
.
А общее уравнение примет вид
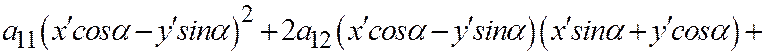
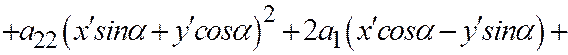
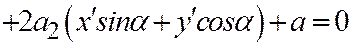 .
.
Или: 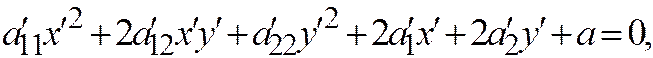
где: 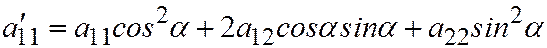 ,
,
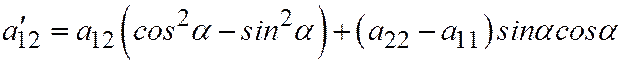 ,
,
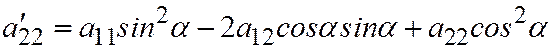 ,
,
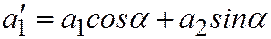 ,
, 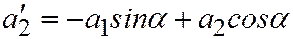 .
.
Условие 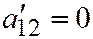 принимает вид:
принимает вид:
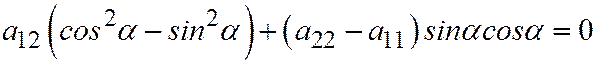 ,
,
Откуда: 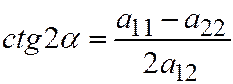 . (2)
. (2)
При повороте на угол 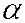 , определяемый этим соотношением, в преобразованном уравнении коэффициент
, определяемый этим соотношением, в преобразованном уравнении коэффициент 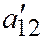 обратится в нуль и оно примет вид:
обратится в нуль и оно примет вид: 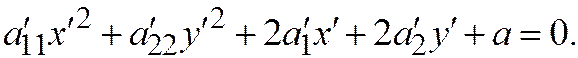 (3)
(3)
I случай. Пусть 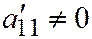 ,
, 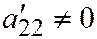 . В уравнении (3) выделим полные квадраты по переменным
. В уравнении (3) выделим полные квадраты по переменным 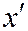 и
и 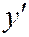 :
: 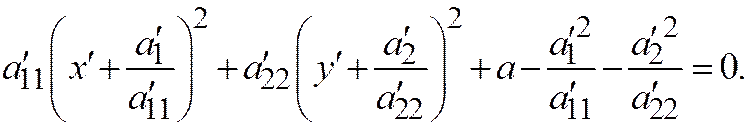 Производя перенос осей координат
Производя перенос осей координат 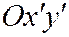 так, чтобы новым началом координат стала точка
так, чтобы новым началом координат стала точка 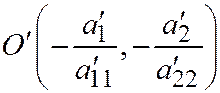 (координаты этой точки даны относительно системы
(координаты этой точки даны относительно системы 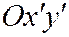 ) и, обозначая новую систему координат через
) и, обозначая новую систему координат через 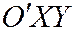 будем иметь:
будем иметь: 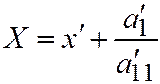 ,
, 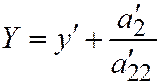 . Так что уравнение (3) примет вид:
. Так что уравнение (3) примет вид: 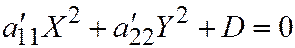 ,
,
где 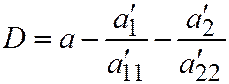 .
.
II случай. Пусть или 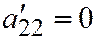 ,
, 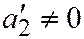 ; или
; или 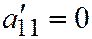 ,
, 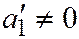 . Предположим, что
. Предположим, что 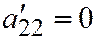 ,
, 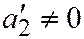 . Тогда уравнение
. Тогда уравнение 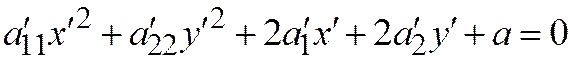 примет вид:
примет вид: 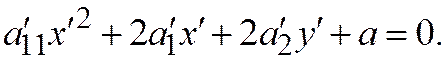 Здесь выделим полный квадрат по переменной
Здесь выделим полный квадрат по переменной 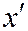 :
: 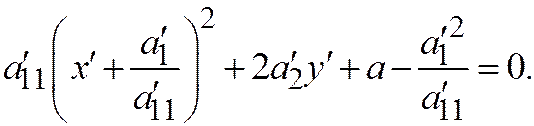 Или:
Или:
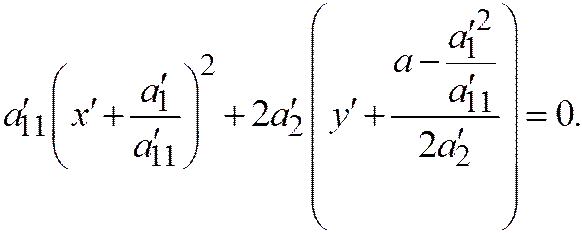
Производя перенос осей координат 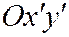 так, чтобы новым началом координат стала точка
так, чтобы новым началом координат стала точка 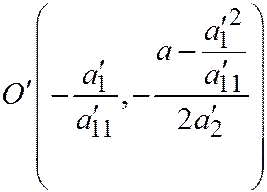 (координаты этой точки даны относительно системы
(координаты этой точки даны относительно системы 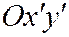 ) и, обозначая новую систему координат через
) и, обозначая новую систему координат через 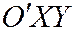 будем иметь:
будем иметь: 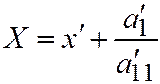 ,
, 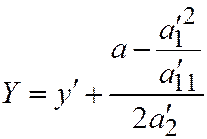 . Так что уравнение (3) примет вид:
. Так что уравнение (3) примет вид: 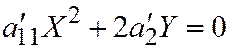 . Это уравнение параболы.
. Это уравнение параболы.
III случай. Пусть или 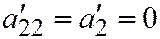 , или
, или 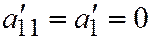 . Предположим, что
. Предположим, что 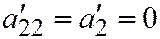 . Тогда уравнение
. Тогда уравнение 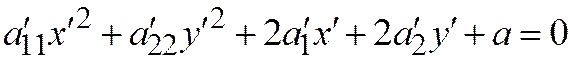 примет вид:
примет вид: 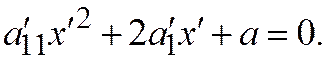 Здесь выделим полный квадрат по переменной
Здесь выделим полный квадрат по переменной 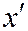 :
: 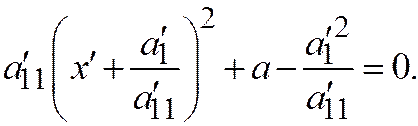 Производя перенос осей координат
Производя перенос осей координат 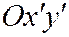 так, чтобы новым началом координат стала точка
так, чтобы новым началом координат стала точка 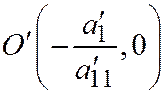 (координаты этой точки даны относительно системы
(координаты этой точки даны относительно системы 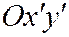 ) и, обозначая новую систему координат через
) и, обозначая новую систему координат через 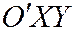 будем иметь:
будем иметь: 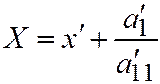 ,
, 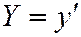 . Так что уравнение (3) примет вид:
. Так что уравнение (3) примет вид: 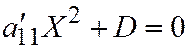 , где
, где 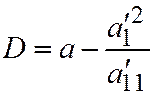 . Это уравнение прямых линий (или двух параллельных, или двух совпадающих). Теорема доказана.
. Это уравнение прямых линий (или двух параллельных, или двух совпадающих). Теорема доказана.
Теорема 2. Общее уравнение линии второго порядка 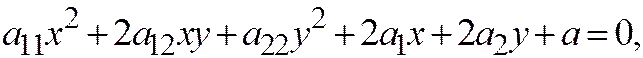
заданной относительно Декартовой прямоугольной системы координат, определяет одну из следующих девяти линий (смотрите таблицу).
Доказательство. По теореме 1 мы с Вами установили, что общее уравнение линии второго порядка может быть приведено к одному из следующих трёх простейших видов:
I. 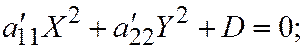 где
где 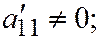
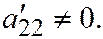 II.
II. 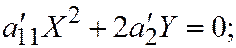 где
где 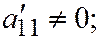
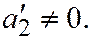
III. 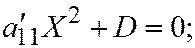 где
где 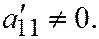
| Группа | № | Уравнение линии | Название линии |
| I | 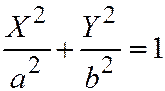
| Эллипс | |
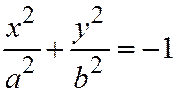
| Мнимый эллипс | ||
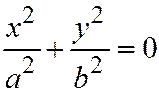
| Две мнимые пересе-кающиеся прямые | ||
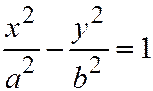
| Гипербола | ||

| Две пересекающиеся прямые | ||
| II | 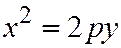
| Парабола | |
| III | 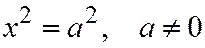
| Две параллел. прямые | |
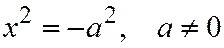
| Две мнимые параллель- ные прямые | ||
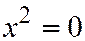
| Две совпад. прямые |
Рассмотрим, какой вид могут принять простейшие уравнения (I), (II), (III) линии второго порядка в зави-симости от знаков коэффициентов этих уравнений.
I. 1. Если 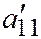 и
и 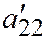 одного знака, а
одного знака, а 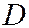 имеет противоположный знак, то деля обе части уравнения (I) на
имеет противоположный знак, то деля обе части уравнения (I) на 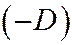 и полагая
и полагая 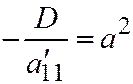 ;
; 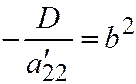 приведём уравнение (I) к виду
приведём уравнение (I) к виду 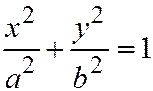 . Это каноническое уравнение эллипса.
. Это каноническое уравнение эллипса.
2. Если 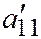 ,
, 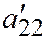 и
и 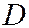 одного знака, то уравнение приводится к виду
одного знака, то уравнение приводится к виду 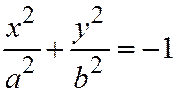 . Это уравнение мнимого эллипса.
. Это уравнение мнимого эллипса.
2. Если 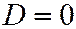 , а
, а 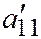 и
и 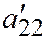 одного знака, то уравнение (I) приводится к виду
одного знака, то уравнение (I) приводится к виду 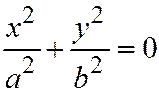 .
.
Это уравнение удовлетворяется только при 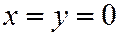 .
.
Но, так как, 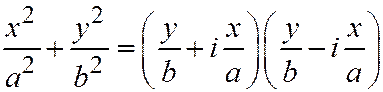 , то говорят, что уравнение (I) распадается на пару мнимых прямых:
, то говорят, что уравнение (I) распадается на пару мнимых прямых: 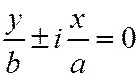 , пересекающихся в действитель-ной точке
, пересекающихся в действитель-ной точке 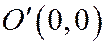 .
.
4. Если 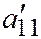 и
и 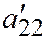 разных знаков, а
разных знаков, а 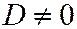 , то уравнение (I) приводится к виду
, то уравнение (I) приводится к виду 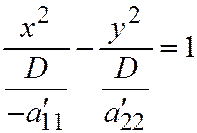 . Считая, что
. Считая, что 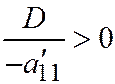 ;
; 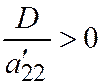 и полагая
и полагая 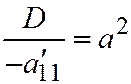 ,
, 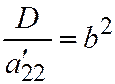 , получим каноническое уравнение гиперболы:
, получим каноническое уравнение гиперболы: 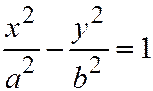 .
.
Если 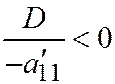 ;
; 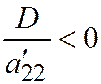 , то получим:
, то получим: 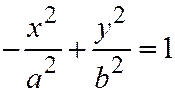 и производя поворот осей координат на угол
и производя поворот осей координат на угол 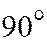 , т.е. полагая
, т.е. полагая 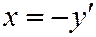 ,
, 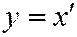 , будем иметь:
, будем иметь: 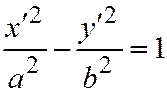 . Это снова каноническое уравнение гиперболы.
. Это снова каноническое уравнение гиперболы.
5. Если 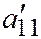 и
и 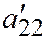 разных знаков, а
разных знаков, а 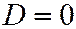 , то уравнение (I) приводится к виду
, то уравнение (I) приводится к виду  и определяет две пересекающиеся прямые:
и определяет две пересекающиеся прямые: 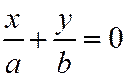 ;
; 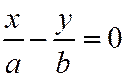 .
.
II. Уравнение (II) можно привести к виду 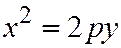 , где
, где 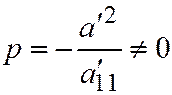 . Число
. Число 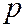 можно считать положительным, так как в противном случае достаточно изменить положительное направление оси
можно считать положительным, так как в противном случае достаточно изменить положительное направление оси  на противоположное.
на противоположное.
III. Уравнение (III) приводится к виду 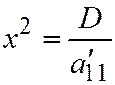 , или
, или 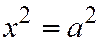 ;
; 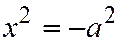 ;
; 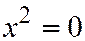 , в зависимости от того, будет
, в зависимости от того, будет 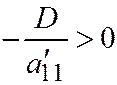 ;
; 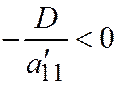 , или
, или 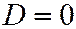 . В первом случае - это будут две параллельные прямые; во втором - две мнимые параллельные прямые; в третьем случае - две совпадающие прямые.
. В первом случае - это будут две параллельные прямые; во втором - две мнимые параллельные прямые; в третьем случае - две совпадающие прямые.
| <== предыдущая лекция | | | следующая лекция ==> |
| Прямолинейные образующие однополостного гиперболоида и гиперболического параболоида. | | | Глава 11. Линии второго порядка, заданные общими уравнениями. Аналитическая геометрия. |
Дата добавления: 2015-08-11; просмотров: 650;
