Глава 11. Линии второго порядка, заданные общими уравнениями. Аналитическая геометрия.
Аналитическая геометрия.
Лекция 8. § 141. Теория инвариантов
Общее уравнение линии второго порядка записывается в следующем виде:
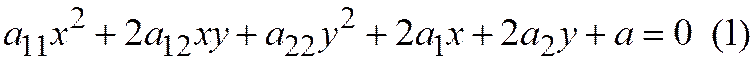
Следующие выражения: 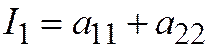 .
. 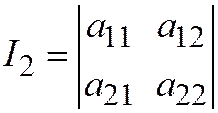 .
. 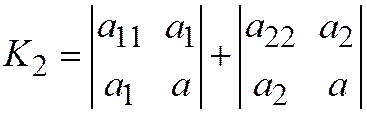 .
.
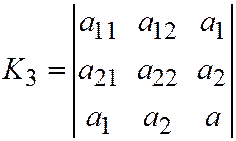 , где
, где 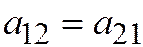 являются инвариантами по отношению к преобразованию одной Декартовой прямоугольной системы координат в другую Декартовую прямоугольную систему координат (ДПСК). Это означает, что если
являются инвариантами по отношению к преобразованию одной Декартовой прямоугольной системы координат в другую Декартовую прямоугольную систему координат (ДПСК). Это означает, что если
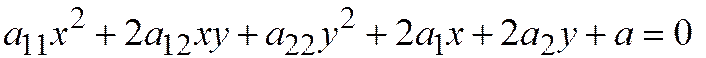 - уравнение линии второго порядка в ДПСК, а
- уравнение линии второго порядка в ДПСК, а
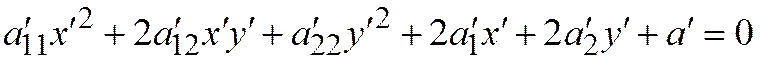
- уравнение той же линии, полученное преобразованием одной ДПСК в другую ДПСК, то: 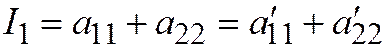 .
. 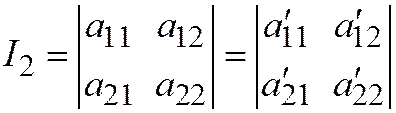 .
. 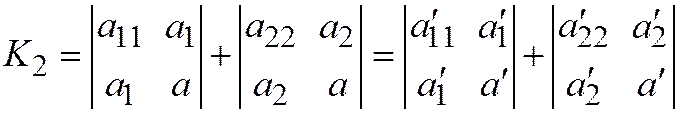 .
.
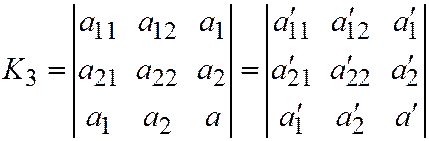 .
.
§ 143. Определение канонического уравнения линии второго порядка при помощи инвариантов. Распадение линии второго порядка на две прямые.
Теорема 1. Для того, чтобы линия второго порядка, заданная общим уравнением относительно ДПСК относилась к первой группе, необходимо и достаточно, чтобы 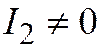 ; ко второй -
; ко второй - 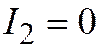 ,
, 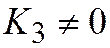 ; к третьей -
; к третьей - 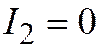 ,
, 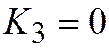 ,
, 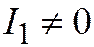 .
.
Доказательство необходимости.
1. Предположим, что линия второго порядка принадлежит к первой группе, т.е. её общее уравнение 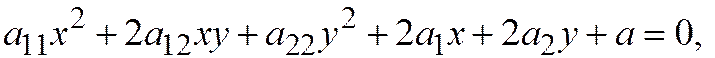 заданное относительно ДПСК, преобразованием прямоугольной системы координат в прямоугольную (т.е. ортогональным преобразованием) может быть приведено к виду
заданное относительно ДПСК, преобразованием прямоугольной системы координат в прямоугольную (т.е. ортогональным преобразованием) может быть приведено к виду
I. 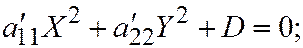 где
где 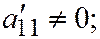
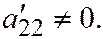 В таком случае:
В таком случае:  .
.
2. Предположим, что линия второго порядка принадлежит ко второй группе, т.е. её общее уравнение заданное относительно ДПСК, преобразованием прямоугольной системы координат в прямоугольную может быть приведено к виду
II. 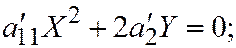 где
где 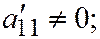
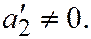
В таком случае: 
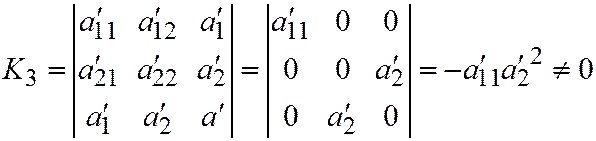 .
.
3. Предположим, что линия второго порядка принадлежит к третьей группе, т.е. её общее уравнение заданное относительно ДПСК, преобразованием прямоугольной системы координат в прямоугольную может быть приведено к виду
III.  где
где 
В таком случае: 
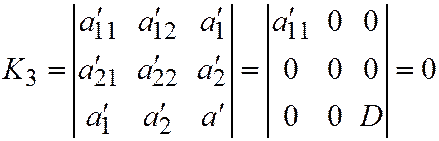 ,
, 
Необходимость доказана.
Доказательство достаточности получается сразу методом от противного. Докажем, например, пункт 1.
1. Предположим, что 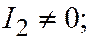 требуется доказать, что линия второго порядка принадлежит к I группе. Предположим, что эта линия принадлежит ко II или III группе; тогда (в силу необходимости)
требуется доказать, что линия второго порядка принадлежит к I группе. Предположим, что эта линия принадлежит ко II или III группе; тогда (в силу необходимости) 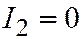 , и мы приходим к противоречию. Аналогично доказывается, что в случае
, и мы приходим к противоречию. Аналогично доказывается, что в случае 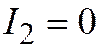 ,
, 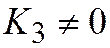 линия принадлежит ко II группе, а в случае
линия принадлежит ко II группе, а в случае 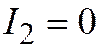 ,
, 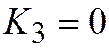 ,
, 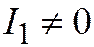 - к III.
- к III.
Теорема 2. Если линия второго порядка задана общим уравнением относительно ДПСК, то её простейшее уравнение имеет вид:
I. 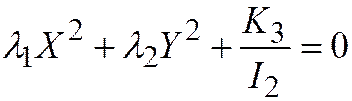 ,
,
II. 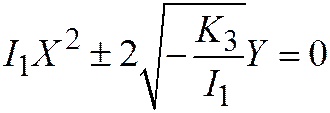 ,
,
III. 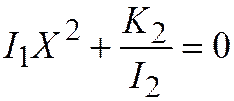 ,
,
Соответственно тому, является ли эта линия I, II или III группы, где 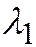 и
и 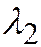 - корни характеристического уравнения квадратичной формы:
- корни характеристического уравнения квадратичной формы: 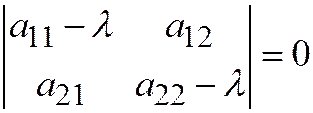 или
или 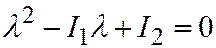 .
.
Доказательство. 1. Пусть линия второго порядка принадлежит к I группе; тогда её простейшее уравнение имеет вид:  , где
, где 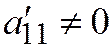 ;
; 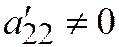 . Находим:
. Находим: 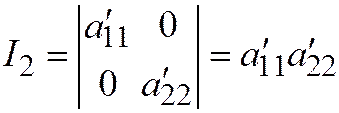 ,
,
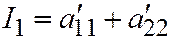 ; так что
; так что 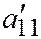 и
и 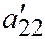 корни
корни 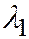 и
и  уравнения
уравнения 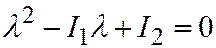 (что следует из теоремы Виета). И, далее:
(что следует из теоремы Виета). И, далее: 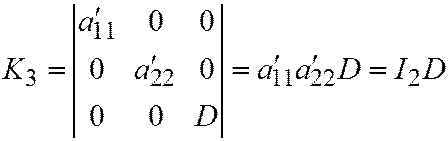 . Откуда:
. Откуда: 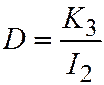 . И мы получаем, что
. И мы получаем, что 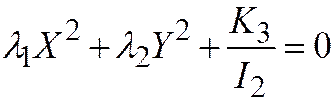 , что в пункте 1 мы и хотели получить.
, что в пункте 1 мы и хотели получить.
2. Пусть линия второго порядка является линией II группы, (т.е. является параболой). Тогда её простейшее уравнение имеет вид: 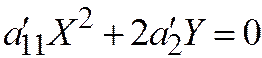 .
.
Находим: 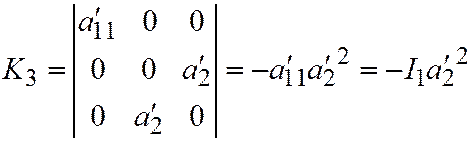 ,
, 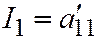 , откуда
, откуда 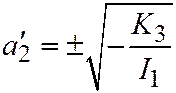 , т.е.
, т.е. 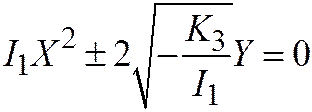 . Пункт 2 доказан.
. Пункт 2 доказан.
3. Пусть, наконец, линия второго порядка является линией III группы, т.е. её простейшее уравнение имеет вид: 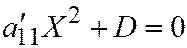 . Находим:
. Находим: 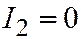 ,
, 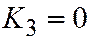 ,
, 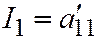 , но для линии III группы
, но для линии III группы 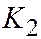 является ортогональным инвариантом, поэтому:
является ортогональным инвариантом, поэтому: 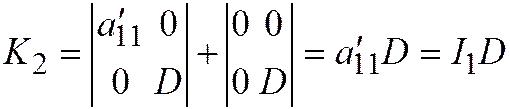 ; откуда:
; откуда: 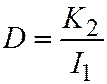 и мы получаем:
и мы получаем: 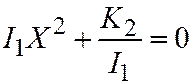 , что и требовалось доказать.
, что и требовалось доказать.
Теорема 3. В следующей таблице даны необходимые и достаточные признаки каждого из девяти классов линий второго порядка.
| Группа | № | Название линии | |
I
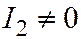
| Эллипс | 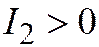 , , 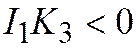
| |
| Мнимый эллипс | 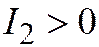 , , 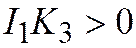
| ||
| Две мн. перес. пр. | 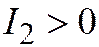 , , 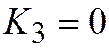
| ||
| Гипербола | 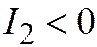 , , 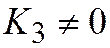
| ||
| Две пересек. прям. | 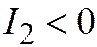 , , 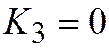
| ||
II
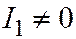
| Парабола | 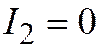 , , 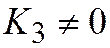
| |
III
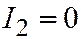
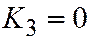
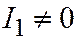
| Две паралл. прям. | 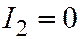 , , 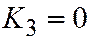 , , 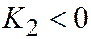 , ,
| |
| Две мн. пар. прям. | 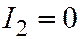 , , 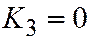 , , 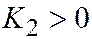 , ,
| ||
| Две совпадающие Прямые | 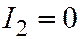 , , 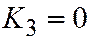 , , 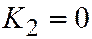 , ,
|
Дата добавления: 2015-08-11; просмотров: 1103;
