Лекция № 3-4
| Определение длины отрезка прямой линиии углов наклона прямой к плоскостям проекций. |
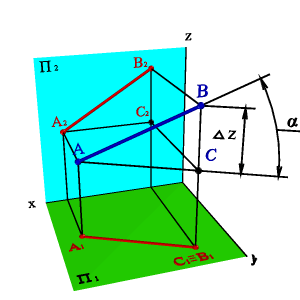
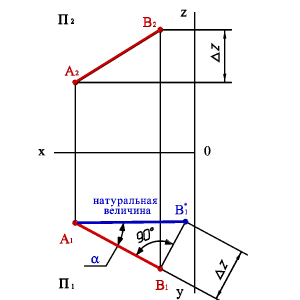
Длину отрезка АВ можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |СB=|ZD, угол a-угол наклона отрезка к плоскости П1, b-угол наклона отрезка к плоскости П2. Для этогона эпюре (рис.3.17) из точки B1 под углом 900 проводим отрезок |B1B1* ZD=|,полученныйв результате построений отрезокA1B1*и будет натуральной величиной отрезка АВ, а угол B1A1B1* =α. Рассмотренный метод называется методом прямоугольного треугольника. Однако все построения можно объяснить, как вращение треугольникаАВСвокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций»
| 
| |
| а) модель | б) эпюр | |
| Рисунок 3.17. Определение натуральной величины отрезка и угла его наклона к горизонтальной плоскости проекций |
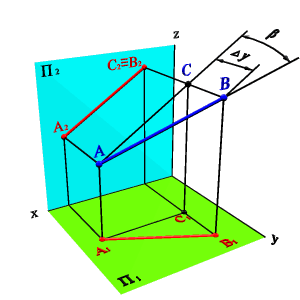
Для определения b-угол наклона отрезка к плоскости П2 построения аналогичные (рис.3.18). Только в треугольнике АВВ* сторона B|В*=|UDи треугольниксовмещается с плоскостью П2.
| 
| |
| а) модель | б) эпюр | |
| Рисунок 3.18. Определение натуральной величины отрезка и угла его наклона к фронтальной плоскости проекций |
Дата добавления: 2015-08-14; просмотров: 714;
