ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Поверхности, выражаемые алгебраическим уравнением второй степени, называют поверхностями второго порядка. Порядок алгебраической поверхности равен степени ее уравнения. Поверхность, определяемая алгебраическим уравнением первой степени, есть плоскость. Среди поверхностей второго порядка выделим:

1.Эллипсоиды. Они имеют каноническое уравнение следующего вида х²/а² + y²/b² + z²/c²=1. Эллипсоиды подразделяются на трехосные (а¹b¹с¹а, рис.10.16), вращения (а=b¹с¹а, рис.10.17) или (а¹b=с, или а=с¹b) и сферу (а=b=c).

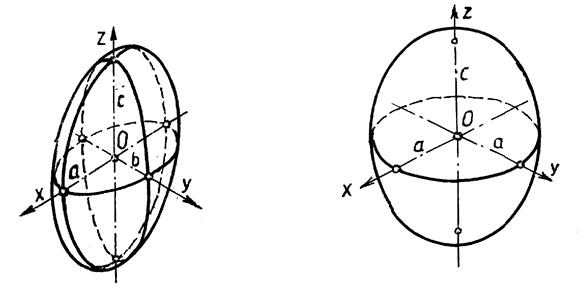
Рис.10.16 Рис.10.17

2. Параболоиды. Параболоиды эллиптические (рис.10.18) имеют уравнение х²/р + y²/b=2z. Параболоид вращения имеет уравнение z²=2px.

3. Параболоиды гиперболические (рис.10.19) имеют уравнение вида: х²/р-y²/q=2z и являются линейчатыми поверхностями (косая плоскость).

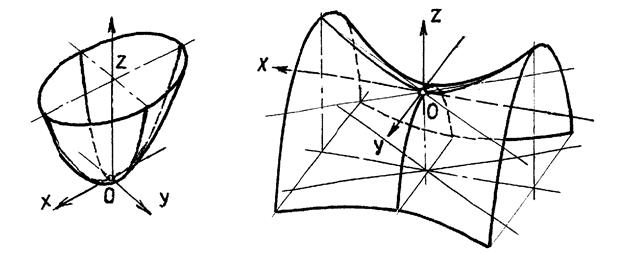
Рис.10.18 Рис.10.19

Гиперболоиды.

а) Гиперболоиды однополостные (рис.10.20) имеют уравнение вида: х²/а²+y²/b²-z²/c²=1 и являются линейчатыми поверхностями.

б) Гиперболоиды двух полостные (рис.10.21) имеют уравнение вида х²/а²+y²/b²-z²/c²=-1.

Гиперболоиды могут быть поверхностями вращения.

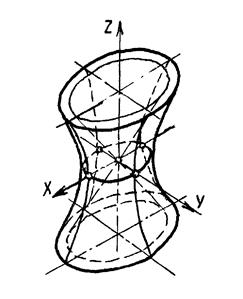
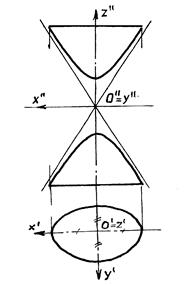
Рис.10.20 Рис.10.21

Поверхности второго порядка могут быть подобными. Два эллипсоида подобны, если отношение их полуосей одинаково: а:b:c=a₁:b₁:c₁. Два эллиптических параболоида подобны, если подобны их сечения плоскостью, перпендикулярной к оси. Два гиперболических параболоида подобны, если их асимптотические плоскости составляют одинаковые углы. Два гиперболоида подобны, если они имеют одинаковые асимптотические конические поверхности.