Межотраслевого баланса

Балансовые модели, как статические, так и динамические, широко применяются при экономико-математическом моделировании экономических систем и процессов. В основе создания этих моделей лежит балансовый метод, т.е. метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них. Если описывать экономическую систему в целом, то под балансовой моделью понимается система уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами количеством продукции и совокупной потребностью в этой продукции. При таком подходе рассматриваемая система состоит из экономических объектов, каждый из которых выпускает некоторый продукт, часть его потребляется другими объектами системы, а другая часть выводится за пределы системы в качестве ее конечного продукта. Если вместо понятия продукт ввести более общее понятие ресурс, то под балансовой моделью следует понимать систему уравнений, которые удовлетворяют требованиям соответствия наличия ресурса и его использования. Кроме приведенного выше требования соответствия производства каждого продукта и потребности в нем, можно указать такие примеры балансового соответствия, как соответствие наличия рабочей силы и количества рабочих мест, платежеспособного спроса населения и предложения товаров и услуг и т. д.

Важнейшие виды балансовых моделей:

· межотраслевые балансы;

· частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей;

· матричные промфинпланы предприятий и фирм.

Балансовый метод и создаваемые на его основе балансовые модели служат основным инструментом поддержания пропорций в народном хозяйстве. Балансовые модели на базе отчетных балансов характеризуют сложившиеся пропорции, в них ресурсная часть всегда равна расходной. Для выявления диспропорций используются балансовые модели, в которых фактические ресурсы сопоставлялись бы не с их фактическим потреблением, а с потребностью в них. В связи с этим балансовые модели не содержат какого-либо механизма сравнения отдельных вариантов экономических решений и не предусматривают взаимозаменяемости разных ресурсов, что не позволяет сделать выбор оптимального варианта развития экономической системы. Этим определяется ограниченность балансовых моделей и балансового метода в целом.

Основу информационного обеспечения балансовых моделей в экономике составляет матрица коэффициентов затрат ресурсов по конкретным направлениям их использования. Например, в модели межотраслевого баланса такую роль играет так называемая технологическая матрица – таблица межотраслевого баланса, составленная из коэффициентов (нормативов) прямых затрат на производство единицы продукции в натуральном выражении. По многим причинам исходные данные реальных хозяйственных объектов не могут быть использованы в балансовых моделях непосредственно, поэтому подготовка информации для ввода в модель является весьма серьезной проблемой. Так, при построении модели межотраслевого баланса используется специфическое понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей все производство данного продукта независимо от ведомственной (административной) подчиненности и форм собственности предприятий и фирм. Переход от хозяйственных отраслей к чистым отраслям требует специального преобразования реальных данных хозяйственных объектов, например, агрегирования отраслей, исключения внутриотраслевого оборота. В этих условиях понятия «межпродуктовый баланс» и «межотраслевой баланс» практически идентичны, отличие заключается лишь в единицах измерения элементов баланса.

Балансовые модели строятся в виде числовых матриц – прямоугольных таблиц чисел. В связи с этим балансовые модели относятся к тому типу экономико-математических моделей, которые называются матричными. В матричных моделях балансовый метод получает строгое математическое выражение. Таким образом, матричную структуру имеют межотраслевой и межрайонный баланс производства и распределения продукции в народном хозяйстве, модели развития отраслей, межотраслевые балансы производства и распределения продукции отдельных регионов, модели промфинпланов предприятий и фирм. Несмотря на специфику этих моделей, их объединяет не только общий формальный (матричный) принцип построения и единство системы расчетов, но и аналогичность ряда экономических характеристик. Это позволяет рассматривать структуру, содержание и основные зависимости матричных моделей на примере одной из них, а именно на примере межотраслевого баланса производства и распределения продукции в народном хозяйстве. Данный баланс отражает производство и распределение общественного продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Принципиальная схема межотраслевого баланса производства и распределения совокупного общественного продукта в стоимостном выражении приведена в таблице 21. В основу этой схемы положено разделение совокупного продукта на две части: промежуточный и конечный продукт; все народное хозяйство представлено в виде совокупности n отраслей (имеются в виду чистые отрасли), при этом каждая отрасль фигурирует в балансе как производящая и как потребляющая.

Таблица 21-Принципиальная схема межотраслевого баланса (МОБ)

Производящая отрасль	Валовая продукция	Потребление по отраслям	Конечная продукция
		…	j	…	n
	Х1	Х11	X12	…	X1j	…	X1n	Y1
	Х2	Х21	X22	…	X2j	…	X2n	Y2
…	…	…	…	I	…	…	…	II …
i	Хi	Хi1	Xi2	…	Xij	…	Xin	Yi
…	…	…	…	…	…	…	…	…
n	Хn	Хn1	Xn2	…	Xnj	…	Xnn	Yn
Чистая продукция	-	Z1	Z2	… III	Zj	…	Zn	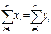IV
Валовая продукция		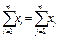X1	X2	…	Xj	…	Xn	-

В МОБ выделяются четыре части, имеющие различное экономическое содержание. Они называются квадрантами баланса (на схеме обозначены римскими цифрами).

Первый квадрант МОБ – это шахматная таблица межотраслевых материальных связей. Показатели, помещенные на пересечениях строк и столбцов, представляют собой величины межотраслевых потоков продукции и в общем виде обозначаются х_ij, где i и j – соответственно, номера отраслей производящих и потребляющих. Так, величина x₃₂ понимается как стоимость средств производства, произведенных в отрасли с номером 3 и потребленных в качестве материальных затрат в отрасли с номером 2. Таким образом, первый квадрант по форме представляет собой квадратную матрицу порядка n, сумма всех элементов которой равняется годовому фонду возмещения затрат средств производства в материальной сфере.

Во втором квадранте представлена конечная продукция всех отраслей материального производства. При этом под конечной понимается продукция, выходящая из сферы производства в область конечного использования (на потребление и накопление). В таблице 21 этот раздел дан укрупненно в виде одного столбца величин Y_i. В развернутой схеме баланса конечный продукт каждой отрасли показан дифференцированно по направлениям использования на личное потребление населения, общественное потребление, на накопление, возмещение потерь, экспорт. Итак, второй квадрант характеризует отраслевую материальную структуру национального дохода, а в развернутом виде – также распределение национального дохода на фонд накопления и фонд потребления, структуру потребления и накопление по отраслям производства и потребителям.

Третий квадрант МОБ также характеризует национальный доход, но со стороны его стоимостного состава как сумму чистой продукции и амортизации. Чистая продукция понимается при этом как сумма оплаты труда и чистого дохода отраслей. Сумму амортизации (c_j) и чистой продукции (v_j + m_j) некоторой j-й отрасли называют условно-чистой продукцией этой отрасли (Z_j).

Четвертый квадрант баланса находится на пересечении столбцов второго квадранта (конечной продукции) и строк третьего квадранта (условно-чистой продукции). Этим определяется содержание квадранта: он отражает конечное распределение и использование национального дохода. В результате перераспределения первоначально созданного национального дохода образуются конечные доходы населения, предприятий, государства. Данные четвертого квадранта важны для отражения в межотраслевой модели баланса доходов и расходов населения, источников финансирования капиталовложений, текущих затрат непроизводственной сферы, для анализа общей структуры конечных доходов по группам потребителей. Общий итог четвертого квадранта, так же как второго и третьего, должен быть равен созданному за год национальному доходу.

Таким образом, в целом межотраслевой баланс в рамках единой модели объединяет балансы отраслей материального производства, баланс совокупного общественного продукта, балансы национального дохода, финансовый баланс, баланс доходов и расходов населения. Хотя валовая продукция отраслей не входит в рассмотренные выше четыре квадранта, она представлена на принципиальной схеме МОБ в двух местах в виде столбца, расположенного справа от второго квадранта, и в виде строки ниже третьего квадранта. Эти столбец и строка валовой продукции замыкают схему МОБ и играют важную роль как для проверки правильности заполнения квадрантов (т.е. проверки самого баланса), так и для разработки экономико-математической модели межотраслевого баланса. Если, как показано на схеме, обозначить валовой продукт некоторой отрасли буквой X с нижним индексом, равным номеру данной отрасли, то можно записать два важнейших соотношения, отражающих сущность МОБ и являющихся основой его экономико-математической модели.

Во-первых, рассматривая схему баланса по столбцам, можно сделать вывод, что итог материальных затрат любой потребляющей отрасли и ее условно-чистой продукции равен валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:

X_j= 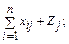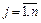(1)

Величина условно-чистой продукции Z_j равна сумме амортизации, оплаты труда и чистого дохода j-й отрасли. Соотношение (1) охватывает систему из n уравнений, отражающих стоимостный состав продукции всех отраслей материальной сферы.

Во-вторых, в схеме МОБ по строкам для каждой производящей отрасли валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:

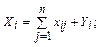
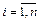(2)

Формула (2) описывает систему из n уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования.

Просуммируем по всем отраслям уравнения (1), в результате получим:

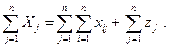
Аналогичное суммирование уравнений (2) дает:

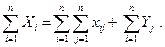
Левые части обоих равенств равны, так как представляют собой весь валовой общественный продукт. Первые слагаемые правых частей этих равенств также равны, их величина равна итогу первого квадранта. Следовательно, должно соблюдаться соотношение

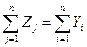(3)

Левая часть уравнения (3) есть сумма третьего квадранта, а правая часть – итог второго квадранта. В целом же это уравнение показывает, что в межотраслевом балансе соблюдается важнейший принцип единства материального и стоимостного состава национального дохода.