Межотраслевого баланса. Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица

Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица является также основой экономико-математической модели межотраслевого баланса. Предполагается, что для производства единицы продукции в j-й отрасли требуется и определенное количество затрат промежуточной продукции i-й отрасли, равное а_ij. Оно не зависит от объема производства в отрасли и является довольно стабильной величиной во времени. Величины а_ij называются коэффициентами прямых материальных затрат и рассчитываются следующим образом:

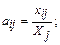
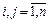(4)

Определение 1. Коэффициент прямых материальных затрат показывает, какое количество продукции i-й отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j-й отрасли.

С учетом формулы (4) систему уравнений баланса (2) можно переписать в виде:

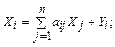
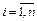(5)

Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А = (а_ij), вектор-столбец валовой продукции 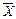и вектор-столбец конечной продукции :

= .

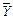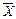то система уравнений (5) в матричной форме примет вид:

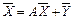(6)

Система уравнений (5), или в матричной форме (6), называется экономико-математической моделью межотраслевого баланса (моделью Леонтьева, моделью «затраты – выпуск»). С помощью этой модели можно выполнять три варианта расчетов:

· задав в модели величины валовой продукции каждой отрасли (X_i), можно определить объемы конечной продукции каждой отрасли (Y_i):

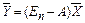(7)

· задав величины конечной продукции всех отраслей (Y_i) можно определить величины валовой продукции каждой отрасли (X_i):

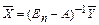(8)

· задав величины валовой продукции для ряда отраслей, а для всех остальных отраслей задав объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. В этом варианте расчета удобнее пользоваться не матричной формой модели (6), а системой линейных уравнений (5).

В формулах (7) и (8) Е обозначает единичную матрицу n-го порядка, а (Е_n-А)^-1 обозначает матрицу, обратную к матрице (Е-А). Если определитель матрицы (Е_n-А) не равен нулю, т.е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через В=(Е_n-А)^-1. Тогда систему уравнений в матричной форме (8) можно записать в виде:

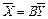(9)

Элементы матрицы В будем обозначать через b_ij. Тогда из матричного уравнения (8) для любой i-й отрасли можно получить следующее соотношение:

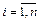(10)

Из соотношений (9) следует, что валовая продукция выступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты b_ij, которые показывают, сколько всего нужно произвести продукции i-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. В отличие от коэффициентов прямых затрат a_ij коэффициенты b_ij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства.

Определение 2. Коэффициент полных материальных затрат b_ij показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.

Коэффициенты полных материальных затрат можно применять, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей:

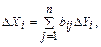i=

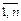
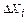и 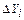- изменения (приросты) величин валовой и конечной продукции соответственно.

Определение полных затрат осуществляется 2-мя способами:

1. Через нахождение обратной матрицы:

a) Методом Жордана-Гаусса:

а₁₁ а₁₂ … а_1n

а₂₁ а₂₂ … а_2n

… … … …

а_n1 a_n2 … a_nn

Присоединяем единичную матрицу E_n. В качестве разрешающего элемента выбирается a_i*j*, где i=j и изменяется от 1 до n.

Пересчет разрешающего столбца:

a^#_i*j*=1, a^#_ij*=0,

Пересчет разрешающей строки:

a^#_i*j=a_i*j / a_i*j*

Остальные элементы пересчитываются по правилу прямоугольника:

a^#_ij = 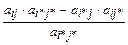, i= 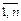, кроме i=i_*, j= 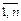, кроме j=j_*.

б) Путем вычисления определителя и присоединенной матрицы:

,

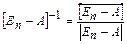где 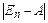- определитель матрицы ,

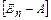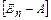- матрица, присоединенная к матрице .

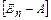Элементами присоединенной матрицы являются алгебраические дополнения элементов определителя матрицы, транспонированной относительно матрицы .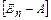

2. Через прямые и косвенные затраты.

Коэффициент полных затрат продукции представляет собой сумму прямых затрат a_ij и косвенных затрат i-й продукции для производства единицы j-й продукции через все конечные продукты на всех предыдущих стадиях производства.

c_ij = a_ij + a⁽¹⁾_ij + a⁽²⁾_ij + … + a^(k)_ij

С = A + A² + A³ + … + A^k+1

B = E_n + C,

т.е. b_ij =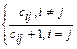

Экономический смысл различия между коэффициентами b_ij и с_ij заключается в том, что в отличие от коэффициента с_ijкоэффициент b_ij включает в себе саму единицу конечной продукции, которая входит в сферу производства. Если выпуск конечного продукта j нужно увеличить на единицу, то валовой выпуск продукта i должен быть увеличен на b_ij.

Для дополнительного выпуска единицы конечной продукции j-го вида валовой выпуск во всех других отраслях должен возрасти на величину полных затрат на производство этой единицы, а в самой отрасли j, кроме того, к валовому выпуску добавляется и эта дополнительно производимая единица.