ТЕРМИЧЕСКОГО УДАРА

Как было указано выше, одним из самых больших недостатков вольфрама является плохое сопротивление термическому удару. Затрачено много усилий для устранения этого недостатка путем подбора формы, размеров, толщин изделий из него с целью ослабления внутренних термических напряжений в материале.

Авторы [43]дают математическое обоснование термостойкости и по приведенной формуле вычисляют внутренние напряжения в образцах вольфрама. В формулу входят измеренные деформации, температура поверхности, геометрические размеры, механические и теплофизические свойства материала.

Общепринятых методик испытаний на термическую стойкость нет. Обычно в каждом конкретном случае условия испытаний пытаются приблизить к натурным. Например, в работе Д. Гордона были взяты трубчатые образцы с наружным диаметром 38 мм, внутренним – 18 мм и длиной 51 мм. Таким образом, толщина стенки образца – 10 мм; с одной стороны к стенке подводилось тепло с удельным потоком: Q=1.3•10⁷Дж/м²•с=1,3•10⁷ Вт/м², с другой – вода.

Образец из псевдосплава W+Agрастрескался с громким шумом через 8 секунд. За критерий термостойкости была взята величина удельного потока Q.

Оказалось, что наилучшей термостойкостью обладают образцы из псевдосплавов вольфрама с серебром и медью. Кованный вольфрам обладает тоже более высокой термостойкостью, чем просто спеченный, но несколько ниже указанных псевдосплавов.

Конечно, большую роль играет скорость нагрева, т.е. dT/dτ.

Авторы приводят формулу для количественного определения параметра термостойкости:

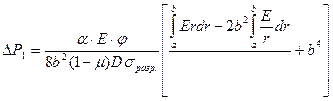
где: α – коэффициент термического расширения; Е – модуль упругости; φ – скорость повышения температуры; b – наружный радиус образца; а – внутренний радиус образца; μ – коэффициент Пуассона;

r – текущее значение радиуса;D=𝜆/(С•γ) – температуропроводность; σ_разг. – разрушающее напряжение.

Чем больше параметр ∆P₁, тем хуже термостойкость. Но кроме указанных величин, входящих в формулу, нужно учитывать:

- порог хрупкости;

- форму и размеры изделий;

- чувствительность к скорости деформации;

- пластичность;

- состояние поверхности;

- чувствительность материала к надрезу;

- внутреннюю структуру материала;

- изменение характеристик с изменениями температуры.

На образец действуют с одно стороны растягивающие напряжения, с другой – сжимающие, в результате чего в образце возникают изгибающие напряжения. Если материал хрупок, под действием последних он растрескивается, если пластичен – происходит перераспределение напряжений внутри образца. При увеличении толщины стенки образца (b-a) параметр ∆P₁ где-то достигает максимума, и толщина становится при этом критической. Для вольфрама она близка к 10 мм, хотя и зависит от структуры, скорости подъема температуры и других характеристик, указанных выше.

Для выбранных образцов в данном случае растрескивание происходит при скорости подъема температуры 1650 к/с для вольфрама, пропитанного медью. Для напряженного и рекристаллизованного материала эта скорость составляет всего 750 К/с. Число концентраторов напряжений можно уменьшить путем предварительного окисления поверхности или шлифования ее. Но это касается вольфрама, непропитанного медью. Отечественный опыт говорит о том, что пропитанные медью образцы нельзя шлифовать, т.к. при этом создается ложная бездефектность поверхности, и это мешает определить настоящее ее состояние при контроле.