Контр жеткізу матрицасы.
Төмендегі ережемен анықталғн Q=(qij)-матрицасын анықтаймыз.
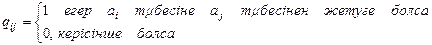
Бұл матрицаның анықталуынан, егер С-жеткізу матрицасы болса, Q=CТ. Бұл екі матрицаларды (Q, C) графтың мықты компоненттерін табуға пайдалануға болады.
S=Q*C матрицасын қарастырамыз , мұндағы * операциясы С мен Q матрицаларының сәйкес элементтерін көбейту дегенді көрсетеді, яғни:
sij=qij * сij
матрицаның ai және aj төбелері өзара жеткізетін төбелер болса, яғни ai 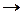 aj, aj
aj, aj 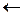 ai болса ғана sij=1.
ai болса ғана sij=1.
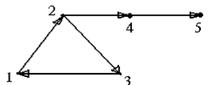
Демек s матрицасы төмендегідей Е эквивалентті қатынас болып табылады: ai мен aj бірге бір мықты компонентте болса ғана ai Е aj орындалады. Демек, ai төбесі бар мықты компонент sij=1 aj элементтерінен тұрады. Суреттегі графтың жеткізуші С матрица сымен контр  жеткізуші Q матрицалары төмендегідей:
жеткізуші Q матрицалары төмендегідей:
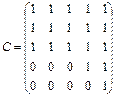 ,
, 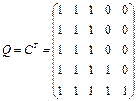 ,
, 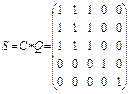
S матрицаның екінші жолы бойынша 2-ші төбе кіретін мықты компонент {1,2,3} төбелерінен тұрады.
Графтағы ең қысқа жолдар (арақашықтық). Айталық, G кез-келген граф, ал х, yÎV(G) оның екі төбесі болсын. х-тен у апаратын маршрутты Р0 деп, ал ұз. Р арқылы х пен у-ті қосатын кез келген маршруттың ұзындығын белгілейік. (ұз. Q арқылы Q маршрутының ұзындығы белгіленеді.).
Анықтама. Егер ұз. Р0≤ ұзындығы Р болса Р0 маршруты ең қысқа маршрут деп аталады.
Ең қысқа жолда төбелер мен доғалар (қабырғалар) қайталанбайды. Шынында да, егер Р0 маршрутында Р0:х=z, e1, z1,….,zp-1, ep, zp=у zi=zj бар болса, онда Р0 маршрутын zі-ден zj-ға дейінгі кесіндіні алып тастап қысқартуға болар еді, яғни Р0 -ді x = z0, e1,...,ei, zi, ej+1,...,zp-1, ep, zp=у маршрутымен алмастырар едік. Сондықтан да шын мәнінде ең қысқа маршрут қарапайым шынжыр болады. «Ең қысқа жол», «Ең қысқа маршрут», «Ең қысқа шынжыр» терминдерінің мағынасы бірдей.
Айталық, G=<M, R> байланысқан бағытталмаған граф, ал а мен b оның әртүрлі төбелері болсын.
Анықтама. Ең қысқа (a, b) -маршруты a, b төбелерінің арақашықтығы деп аталады және 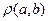 мен белгіленеді.
мен белгіленеді.
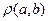 =0 (анықтама бойынша арақашықтық 0 ге тең болсын). Бұлай анықталған арақашықтық метриканың төмендегідей аксиомаларын қанағаттандырады.
=0 (анықтама бойынша арақашықтық 0 ге тең болсын). Бұлай анықталған арақашықтық метриканың төмендегідей аксиомаларын қанағаттандырады.
- 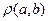 ≥0;
≥0;
- 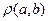 = 0‹═›a=b;
= 0‹═›a=b;
- 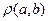 =
=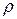 ( b, a) (симметриялық);
( b, a) (симметриялық);
- 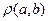 <
< 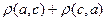 (үшбұрыш теңсіздігі)
(үшбұрыш теңсіздігі)
Анықтама. Егер M={a1, a2, …, an} төбелер жиыны болса, онда элементтері Pij =(рij) арақашықтықтар арқылы анықталатын рij= 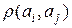 матрицасы арақашықтық матрицасы деп аталады. PT=P, яғни Р-симетриялы матрица.
матрицасы арақашықтық матрицасы деп аталады. PT=P, яғни Р-симетриялы матрица.
Анықтама. Тұрақты бір а төбесі үшін e(a) 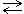 max{
max{ 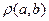 │b
│b 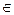 M} а төбесінің эксцентриситеті деп аталады. Яғни төбелердің эксцентриситеті осы төбемен одан ең алыс жатқан төбенің арақашықтығы.
M} а төбесінің эксцентриситеті деп аталады. Яғни төбелердің эксцентриситеті осы төбемен одан ең алыс жатқан төбенің арақашықтығы.
Егер Р арақашықтық матрицасы болса онда e(ai) эксцентриситеті і-ші жолда орналасқан сандардың ең үлкеніне тең. Төбелері эксцентриситеттерінің ішіндегі ең үлкені G графының диаметрі деп аталады және ол d(G) болып белгіленеді; d(G)=max{e(a)│a 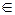 M}
M}
Анықтама. Егер e(a)=d(G) болса а төбесі перийфериядағы төбе деп аталады Мысал :
Суреттегі G графының диаметрін табу керек.

Анықтама. Эксцентриситеттердің ең кішісі графтың радиусы деп аталады r(G) болып белгіленеді; r (G) 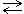 min{e (a)│a
min{e (a)│a 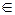 M};
M};
Анықтама. Егер e(a)=r(G) а төбесі орталық төбе деп аталады. Барлық орталық төбелердің жиыны графтың центрі деп аталады. Мысалы, жоғарыдағы графтың радиусы 2-ге тең r(G)=2, центрі {2, 4, 5} жиыны болады.
Орталық төбелерді табу есебі іс жүзінде көптеп кездеседі. Мысалы граф – төбелері елді мекендер, қабырғалары олардың арасындағы жолдарды білдіретін – жолдар желісін өрнектейтін болсын.Ауруханаларды, қызмет көрсету пунктерін т.б. тиімді орналастыру керек. Тиімділік дегенді бұл жерде қызмет көрсететін пункттен неғұрлым алыс орналасқан елді мекендердің ара қашықтығын неғұрлым азайту болып табылады. Демек, графтың орталық төбелері больница, қызмет көрсету пункттерін орналастыратын орындар болып табылады. Нақтылы есептерде бұларға қоса елді мекендердің ара қашықтығын, жолға кететін уақыт, жол бағасын т.б. ескеруге тура келеді. Бұл параметрлерді ескеру үшін салмақталған графтар қолданылады. Айталық G=<M, R> әр (a, b) доғасының салмағы 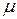 (a, b) нақты санына тең салмақтанған граф болсын.
(a, b) нақты санына тең салмақтанған граф болсын.
Анықтама.a1, a2,…,an, an+1 маршрутының салмағы деп 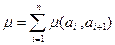 санын айтады. (a, b)- маршрутының салмақтарының ең кішісі а және b төбелерінің салмақтанған арақашықтығы деп аталады
санын айтады. (a, b)- маршрутының салмақтарының ең кішісі а және b төбелерінің салмақтанған арақашықтығы деп аталады 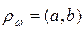 болып белгіленеді.
болып белгіленеді.
Анықтама. Салмағы 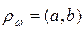 арақашықтығына тең (a, b) маршруты салмақтанған G графындағы ең қысқа маршрут деп аталады.
арақашықтығына тең (a, b) маршруты салмақтанған G графындағы ең қысқа маршрут деп аталады.
Анықтама. а төбесінің салмақтанған эксцентриситеті деп max{ 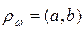 │b
│b 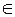 M} санын айтады, оны
M} санын айтады, оны 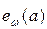 деп белгілейді.
деп белгілейді.
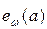 =max{
=max{ 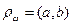 │b
│b 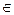 m}
m}
Анықтама. G графының салмақтанған орталық төбесі деп 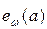 =min{
=min{ 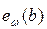 │b
│b 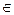 M} а төбесін айтады.
M} а төбесін айтады.
Анықтама. Орталық төбенің салмақтанған эксцентриситеті G графының салмақтанған радиусы деп аталады , 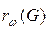 болып белгіленеді.
болып белгіленеді.
Мысалы: Салмақтанған орталық төбе Новосибирск 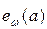 =274, ал
=274, ал 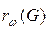 =681
=681
Графтағы ең қысқа маршрутты анықтайтын өте қарапайым әрі тиімді алгоритм бар.
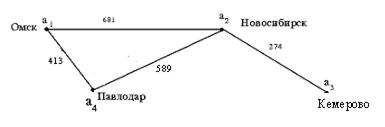
Оны бұрыннан белгілі бас қатырғыш жұмбақ есеп мысалында қарастырайық. Екі адамда вино құйылған 8 литрлік бір құмыра және 5 литрлік, 3 литрлік екі бос құмыра бар. Виноны құмыралар не толық, не бос болатындай құйып, екі адам барлық виноны тең бөлісуі керек.
Алдымен екі мүмкіндікті қарастырамыз: 8 литрлік құмырадан вино 5 литрлік және 3 литрлік құмыраларға құйылады. Бұл мүмкіндіктерді символдық түрде 800→350 және 800→503 деп белгілейік. Құмыраларға виноны құюдың әртүрлі мүмкіндіктерін (х,у,z) үштігімен немесе қысқаша хуz деп белгілейміз. Мұндағы х – 8 литрлік құмырадағы вино, у–5 литрлік құмырадағы вино және z – 3 литрлік құмыраға құйылатын вино. 350 жағдайында 3 түрлі құю мүмкіндігі бар: 350→323, 350→053, 350→800. Осындай ситуацияларға талдау жасай келе және құмыраларды түрліше толтыра отыра суретте көрсетілгендей бағытталған граф аламыз. Алынған графтың төбелері ретінде әртүрлі жағдайларды сипаттайтын үштіктер ал виноны түрліше құюлар доғаларға сәйкес келеді. Әрине, бұлграфта еселі доғалар жоқ, яғни бұл диграф. Жалпы, ең қысқа маршрутты анықтау есептеріндегі графтарда ілгектер мен еселі қабырғалар (доға) жоқ деп алынады. 800 төбеден 440 төбесіне апаратын маршрут табылса есеп шешілді деп есептейміз. Суреттен мұндай жол оңай табылатындығын көреміз: 800, 350, 323, 620, 152, 143, 440. Бұл жолға есептің шешімін беретін төмендегідей құюлар сәйкес келеді.
Вино 8 литрлік құмырадан 5 литрлік құмыраға толтырылады.
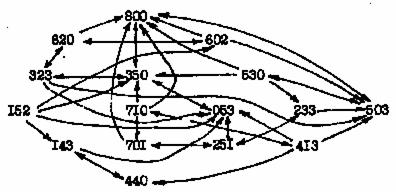
1-Сурет. Түрлі жағдайлар мен құюлар графы.
Содан кейін 5 литрлік құмырадан вино 3 литрлік құмыра толғанға дейін құйылады. 3 литрлік құмырадан вино түгелдей 8 литрлікке құйылады. 5 литрліктегі 2 литр 3 литрлікке құйылады. 8 литрліктегі 5 литрлікке толтырылады. 5 литрліктен 1 литрді 8 литрлік құмыраға құю керек (толғанға дейін). Соңында 3 литрліктен барлық виноны 8 литрлік құмыраға құйылады. Нәтижесінде 8 литрлік құмырада 4 литр вино және сонша литр 5 литрлік құмырада болады. Вино тең бөлінді.
Осы 800 төбеден 440 төбеге апаратын жол ең қысқа болады. Бұл жолды графтардағы ең қысқа маршрутты анықтайтын алгоритмді пайдаланып та табуға болады. Енді осы алгоритмнің жұмысын формальды түрде сипаттап көрейік:
Алгоритмнің жұмысы барысында х0=800 алғашқы төбеден бірдей қашықтықтағы төбелер жиыны құрылады. Бұл жиындарды вертикаль түзулер яғни ярустарға (2 сурет) орналастырамыз (2-сурет). Нөлінші яруста бір ғана х0=800 төбесі орналасқан. Бірінші яруста 800-ден шығатын доғалар кіретін төбелер орналасқан (350 және 503). Екінші ярусқа 350 және 503 төбелерге сыбайлас, бірақ 0-ші немесе 1-ші ярустарға кірмейтін төбелерді белгілейміз. Егер k-шы ярус құрылған болса (k+1)-ярусқа G графының алдыңғы ярустарда жоқ және k-шы ярустағы төбелерге сыбайлас төбелерді енгіземіз. Ярус құру у0=440 төбесі алынған сәтте тоқталады.
Осыдан кейін құрылған графтың у0=440 төбесінен х0=800 төбесіне қайту барысында маршрутты анықтаймыз. Бұл маршрутпен кері жүру барысында х0=800 төбесінен у0=440 төбесіне апаратын ең қысқа жол табылады.
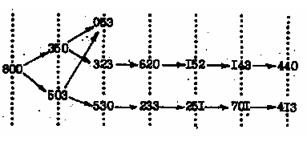
2-сурет "Ярусты" граф
Біз ең қысқа жолды табу алгоритмін 1-суреттегі графқа қолданылатындай сипаттадық. Нақтылы бір мысалға жазылған бұл алгоритмді кез келген графқа қолдануға болатындай алгоритмнің сипаттамасын келтірейік: Al1 алгоритмін графтың берілген екі төбесін қосатын ең қысқа маршрутын табу үшін сипаттаймыз. Бұл алгоритмнің негізіне берілген графтың бір төбесінен шығатын ең қысқа жолдардың графы деп қарастыруға болатын ярустық граф құру алгоритмі жатады. Сондықтан алдымен ең қысқа жолдардан құралған ішкі граф құратын Al2 алгоритмін сипаттайық:
Al2 алгоритмі (ең қысқа жолдар графын құрады).
Басы. Бағытталған G графы және оның бір х0ÎV(G) төбесі берілген. G графын кіретін және шығатын аймақтар {O+(х), O-(х)|xÎV(G)} үйірімен берейік.
1. L:={x0}, M:=Æ, Г(x0):=Æ, h(x0):=0, t:=0;
Мұндағы L мәндері құрылғалы тұрған ағымдағы яруста жатқан төбелер жиыны болатын айнымалы; М-мәндері құрылғалы тұрған ағымдағы ярустың алдындағы яруста орналасқан төбелер жиыны болатын айнымалы; Г әрбір х төбесіне құрылатын графтың х–ке апаратын төбелер жиынын белгілейтін функция; h xo төбесінен x төбесіне дейінгі аралықты көрсететін натурал санды кез келген x төбесіне белгілейтін функция; t- h функциясын есептеуге қолданылатын бүтін мәнді айнымалы t.
2. M:=MUL;
3. Әрбір zÎL, t:=t+1; L:=È{O-(x)|xÎL}\M, Г(z):=O+(z)ÇМ, Г(z):=t+1;
4. Тексеру: L=Æ. Егер дұрыс болса 2 пунктке көш.
Соңы. М, h және Г баспаға бер.
Мұнда М xo төбесінен шығатын ең қысқа жолдар графының төбелер жиыны; Г(х) ең қысқа жолдар графынан шығатын х төбесінің аймағы.
h(х)–G графындағы ρ(х0, х) арақашықтығы(х пен у төбесінің арақаш-ықтығы деп х пен у-ті қосатын ең қысқа жолды айтады).
1-кесте
| X | ||||||||||||||||
| Г | ||||||||||||||||
| H |
AL2 алгоритмін х0-800 төбесімен G басқатырғыш графына қолданғанда 26 қадам жүргізіледі, оған қоса М айнымалысының ең соңғы мәні Г және h функцияларының мәндерімен берілген 1-кестеде көрсетілген жиын болады. 1-кестеде шын мәнінде х0-800 төбесінен шығатын ең қысқа жолдар графы көрсетілген. (Г(х) бұл графта х төбесінің кір етін аймағы).
х0 төбесінен у0 төбесіне жеткізетін ең қысқа жолды табу үшін кестеден Г(у0) мәнін табамыз және одан қандай да бір у1ÎГ(у0) төбесін аламыз. у1 төбесі үшін Г(у1) мәнін табамыз да, одан қандай да бір у2ÎГ(у1) төбесін аламыз. Осылай жалғастыра келе х0 төбесіне келеміз ( бұл төбе үшін Г(х0)=0). Мысалы, у0=440 алсақ мынадай тізбек аламыз: у0=440, у1=143ÎГ(440), у2 =152ÎГ(143), у3=602ÎГ(143), у4=620ÎГ(602), у5=323ÎГ(620), у6=350ÎГ(323), у7=800, Г(800)=0. Демек, 800 төбесінен 440 төбесіне жеткізетін ең қысқа маршрут: 800, 350, 323, 620, 602, 152, 143, 440.
Графтың екі төбесінің арасындағы ең қысқа жолды анықтайтын Al1 алгоритмін Al2 алгоритмінен жеңіл шығарып алуға болады.
Al1 алгоритмі (графтың екі төбесінің арасындағы ең қысқа жолды анықтайды)
Басы. G бағытталған граф, х0, у0 оның екі төбесі
Al2 алгоритмін (G, х0) жұбына қолдану.
у:=у0, u:u=у0.
Мұнда құрылып жатқан ең қысқа жолдың ағымдағы төбесі у-тің мәні болады.
Г(у) табу және Г(у)=0 екендігін тексеру. Егер шарт дұрыс болса, «х0-ден у0-ге апаратын жол жоқ» деген хабар баспаға шықсын.
x0ÎГ(у). екендігін тексеру. Егер дұрыс болса, соңына көш.
Қандай да бір zÎГ(у) төбесін алу. Анық болу үшін Г(у) тізіміндегі бірінші төбені аламыз да у:=z және u:=z,u 3 қадамға көш.
Мұндағы z,u z-ті u тізбегінің басына қосқандағы нәтижені білдіреді.
Соңы. U тізбегін баспаға шығару.
Негізгі әдебиет: [161-180]; 2[108-114] .
Қосымша әдебиет: 7[88-130] .
Бақылау сұрақтары:
1. Маршруттың, шынжырдың, қарапайым шынжырдың, тұйық мар-шруттың, циклдың, қарапайым циклдың анықтамаларын беріңіз.
2. Маршрут ұзындығы не?
3. Қандай граф байланысты деп аталады?
4. Граф төбелерінің арасындағы ұзындығы к-ға тең маршруттың бар екендігін қалай анықтауға болады?
5. Графтың екі төбесін қосатын ең қысқа жолды табудың алгоритмі.
14–дәріс тақырыбы. Эйлер және Гамильтон циклдары (2 сағат)
Дәріс конспектісі: Графтар теориясына негіз болған есептердің бірі Кенигсберг көпірлері туралы есеп. 1-Суретте Леонард Эйлердің тұсындағы(17 ғасыр) XVII ғасырдағы Кенигсберг қаласының картасы салынған. Қала Прегель өзенінің екі жақ жағалауында және 2 аралда. орналасқан Аралдар өзара және жағалаулармен 7 көпірмен жалғасқан. Кенигсберг тұрғындарының арасында сол кезде Кенигсберг көпірлері деп аталатын есеп кең тараған:
Есеп. Үйден шығып әр көпірмен бір рет қана жүріп үйге қайтып келуге болама ма деген сұрақ туады?
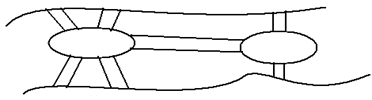
3-сурет
Бұл есеп үшін көпірлерден өтудің маңызы бар. Сондықтан көпірлердің орналасуын 2-суреттегі бағытталмаған мультиграфпен алмастыруға болады. Бұл графта Б, В төбелері өзеннің жағаларына, ал А, Г төбелері аралдар, ал мультиграфтың қабырғалары көпірлерге сәйкес келеді. Егер G графында оның барлық қабырғалары арқылы өтетін цикл табылса Кенигсберг туралы есеп шешілді деп есептеледі (Цикл деп бірде бір қабырға қайталанбайтын циклды маршрутты айтатынын еске саламыз). Демек графтар тілінде есептін қойылуы төмендегідей: Мультиграфта оның барлық қабырғалары болатындай цикл бар ма? Атақты ғалым-математик Л. Эйлер байланысты, бағытталмаған мультиграфта оның барлық қабырғалары болатындай цикл болудың шартын анықтап дәлелдеп берді.
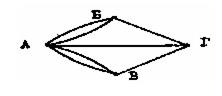
4-сурет
ТеоремаБайланысты бағытталмаған мультиграфтың әр төбесінің дәрежесі жұп сан болса ғана Эйлер циклы болады.
Анықтама. Мультиграфтың барлық қабырғалары болатын цикл Эйлер циклы деп, ал Эйлер циклы бар граф Эйлер графы деп аталады. Жоғардағы суреттегі мультиграфта Эйлер циклы жоқ, себебі онда дәрежесі тақ төбе бар. Айталық ондай цикл бар деп жориық. Олай болғанда бұл циклдың бойымен жүре отыра графтың кез келген төбесіне одан шығу қанша болса сонша рет кіреміз. Демек, G графының әр төбесінің дәрежесі жұп болуы керек. G графында керісінше барлық төбелер тақ дәрежелі.
Бұл тұжырым кез келген бағытталған G графына да жарамды. Сонымен бағытталмаған G графында оның барлық қабырғалары арқылы өтетін цикл бар болу үшін G графының төбелерінің дәрежесі жұп болуы қажетті.
Анықтама. Бағытталмаған (бағытталған) G графындағы цикл оның барлық қабырғалары арқылы өтсе, ол- Эйлер циклы деп аталады. Бағытталмаған графта Эйлер циклы бар болу үшін бұл графтың байланысты болуы қажетті.
Анықтама. Кез келген х,уÎV(G) төбелерін қосатын жол бар болса бағытталмаған G графы байланысты граф деп аталады.
Анықтама. Егер С циклы Бағытталмаған G графының барлық қабырғалары арқылы өтетін болса, кез-келген х,у 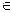 V(G) төбелері үшін C циклының х төбесінен у төбесіне апаратын C(x,y) кесіндісі х-тен у-ке апаратын жол болып табылады. Олай болса G байланысты. Эйлер циклының бар болуы үшін графтың дәрежелерінің жұп болуы және оған қоса графтың байланысты болуы жеткілікті екен.
V(G) төбелері үшін C циклының х төбесінен у төбесіне апаратын C(x,y) кесіндісі х-тен у-ке апаратын жол болып табылады. Олай болса G байланысты. Эйлер циклының бар болуы үшін графтың дәрежелерінің жұп болуы және оған қоса графтың байланысты болуы жеткілікті екен.
Эйлер теоремасы. Бағытталмаған графта Эйлер циклы болу үшін оның байланысты болуы және оның барлық дәрежелерінің жұп болуы қажетті және жеткілікті.
Эйлер теоремасын шамалы өзгеріспен бағытталған графтарға да қолдануға болады. Ол үшін бағытталған графтардың да байланысты болу ұғымын енгізу керек.
Доғаларының бағыттарын алып тастағаннан кейінгі алынған бағытталмаған G графы байланысты болса, бағытталған °G графы байланысты деп аталады.
Теорема.Бағытталған G графында Эйлер циклы болу үшін оның әр төбесіне кіретін дәрежемен шығатын дәрежелердің бірдей болуы қажетті және жеткілікті. дәр.+(х) = дәр.- (х) барлық xÎV(G).
Байланысты және тиелген бағытталмаған графтағы белгіленген V0 және Vn төбелерін қосатын ең қысқа жолды іздеуді жүзеге асыратын Форд алгоритмі.
V0 төбесіне λ0 таңбасы беріледі де, қалған төбелердің таңбалары λ=∞V0 болады.
(Vi, Vj) қабырғаларының ішінен λj – λi>L((Vi, Vj)) орындалатындай қабырғалар ізделеді және олардың λj индекстері λj'=λi+L((Vi, Vj )) алмастырылады. Индекстрді өзгерту процесі одан әрі λj таңбасын азайту мүмкіндігі болмайтын бірде бір қабырға қалмағанша жүргізіледі. Нәтижесінде әр төбенің таңбасы осы төбенің V0 төбесіне дейінгі ең қысқа қашықтықты көрсетеді. Ең қысқа жолдың өзін табу үшін Vn төбесінен екі жағындағы төбелердің таңбаларының айырымы қабырғаның ұзындығына тең қабырғалардың бойымен қозғалу қажет.
Гамильтон циклдары.Гамильтон циклдары туралы есептің интерпритациясы ретінде ең көп тараған коммивояжер туралы есепті қарастыруға болады.
Коммивояжер аралайтын бірнеше қалалардың арақашықтықтары белгілі.
Барлық қалаларда бір реттен ғана болып алғашқы шыққан қаласына қайтып келетін маршрутты табу керек. Егер мұндай маршруттар бірнешеу болса, олардың ең қысқасын табу керек. Мұндай есептер іс жүзінде жиі кездеседі, мысал үшін өндіріс өнімдерін сауда орталықтарына ең қысқа жолмен жеткізу есебі.
Мұндай есептерді шешудің жалпы ортақ теоремалары мен көлемі жөнінен шағын, әрі тиімді алгоритмдердің жоқтығы есепті шешуде қиындықтар туғызады.
Анықтама. Айталық G(V,E) байланысты бағытталмаған граф. G графының барлық төбелері арқылы өтетін, басталуы мен аяқталуы әр түрлі төбелерде болатын қарапайым цикл Гамильтон циклы деп аталады.Графтарда Гамильтон циклдары мен шынжырлары бар болудың жеткілікті шартын келтірейік. Айталық дәр. v–v 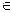 V төбесінің дәрежесі болсын.
V төбесінің дәрежесі болсын.
Теорема. Егер G (V, E), мұндағы |V|=n графында кез келген төбелер vi және vj жұбтары үшін дәр.vi +дәр.vj≥n-1, орындалса, графта гамильтон шынжыры бар, ал егер дәр.vi +дәр.vj≥n немесе дәр.vi≥n/2 графта Гамильтон циклы бар.
Негізгі әдебиет: 2 [20-22]; 3[108-144].
Қосымша әдебиет: 7[88-130] .
Бақылау сұрақтары:
1. Цикл деп нені айтамыз?
2. Қандай граф Эйлер графы деп аталады?
3. Графтың Эйлер графы болуының жеткілікті және қажетті шартын атаңыз?
4. Гамильтон шынжыры, Гамильтон циклы дегендер не?
5. Коммивояжер есебін шешудің қандай алгоритмі белгілі?
15-дәріс. Транспорттық желілер. (2 сағат)
Дата добавления: 2015-08-14; просмотров: 3588;
