Графтың байланыс компоненттері.

Анықтама.Бірдей емес екі төбесі ( 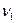, 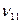) 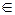G маршрутпен қосылған ( 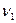-басы, 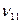-соңы) бағытталмаған G графы байланысты граф деп аталады.

Анықтама: Егер бағытталмаған G графының әртүрлі а,в төбелері үшін (а,в) және в,а)маршруттары бар болса,онда G мықты байланысқан граф деп аталады.

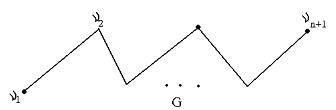
Мұндай ұғымды мультиграф үшін де енгізуге болады.

Мысалдар:

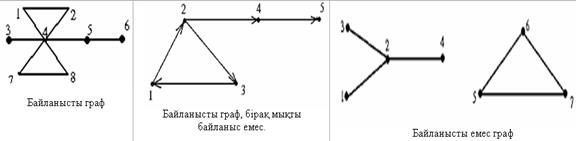
Кез келген байланысты бағытталмаған графтар мықты байланысқан граф екендігін байқауға болады.

Маршрутпен байланысты төбелер қарапайым шынжыр мен де байланысқан болады.

Байланыстылық қатынастың эквиваленттік қасиеті бар және ол граф төбелерін өзара қиылыспайтын V_i, i=1, 2,…,k ішкі жиындарға бөлінуін анықтайды. Сондықтан барлық ішкі графтар G(V_i) байланысқан және олар графтың байланыс компоненттері деп аталады. Бағытталған G графы доғалардың бағыты ескерілмесе байланысқан делінеді, ал егер кез келген V¹ төбесінен V¹¹ төбесіне жол болса мықты байланысқан болады.

Мысалы, мына суреттегі графта екі {1, 2, 3, 4} және {5, 6, 7} байланыс компонент тері бар. Ал мына төмендегі суреттегі бағытталған графта{1,2,3},{4}және {5} төбелерімен берілген 3 мықты компоненттері бар.

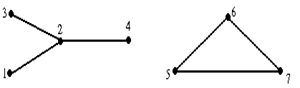
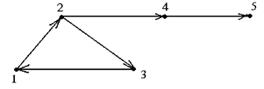
Теорема.Кез келген графты қиылыспайтын байланыс компоненттерінің бірігуімен өрнектеуге болады. Графтың байланыс компоненттеріне жіктелуі бір мәнді анықталады. G=U_i G(V_i)

Сонымен, төбелердің байланысты компоненттері мен мықты компоненттер жиыны төбелер жиындарын бөлшектейді, ал байл. компоненттерінің саны бір мәнді анықталады.

Келесі теорема сыбайлас A_G матрицасы бойынша G графының маршруттарын зерттеуге мүмкіндік береді.

Теорема. Егер A_G-G графыың іргелестік матрицасы болса, онда 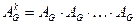матрицасының (i, j)-ші элементі ұзындығы к-ға тең (а_i,j)-маршруттарының санын анықтайды.

Салдар. A_G+ 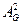+…+ 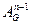матрицасының (i,j)-ші элементі 0-ге тең болмаса ғана n қуатты G графында a_i төбесі ішінде болатын (a_i,a_j) - маршрут (a_i≠a_j) бар.

Мысалы. Сыбайлас A_G матрицаның көмегімен G графында (1,3) маршрутының бар екендігін анықтаймыз.

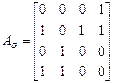
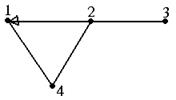
(1,3)- элемент 0-ге тең, демек ұзындығы 1-ге тең маршрут жоқ

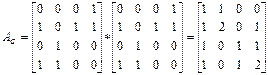
(1,3)-элемент тағыда 0-ге тең. Ұзындығы 2-ге тең (1,3)-маршруты жоқ Ұзындығы 3-ке тең (1,3)-маршруттың саны 1-ге тең

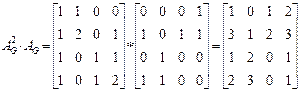
Графтың суретінен бұл маршрут (1, 4, 2, 3) төбелерімен анықталады. Бұл тізбекті іргелестік матрицаны көбейту арқылы алуға болады: 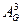матр-ң (1, 3) элементі 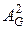матр-ң (1, 2) элементімен A_G матрицаның (2, 3) элементін көбейткеннен алынады.

Өз кезегінде 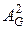м-ң (1, 2) элементі A_G матрицаның (1, 4) эл-н A_G (4,2)-ге көбейткеннен алынды. Демек 1-ден 3-ке жылжи отыра үш қадамнан кейін (1, 4, 2, 3) маршруты алынады.

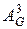матриц-да (4, 2) элементі 3 ке тең, демек, ұзындығы 3 ке тең (4, 2)- маршрутының саны үшеу. Олар:(4, 1, 4, 2), (4, 2, 4, 2), (4, 2, 3, 2)

Граф төбелерінің арасында ұзындығы к-ға тең маршруттың (жол) бар жоғын анықтайтын алгоритмді қарастырайық:

Айталық, 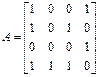төбелері υ1, υ2, υ3, υ4 бағытталған G графының сыбайлас матрицасы болсын. 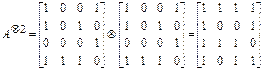матрицасын қарастырайық. Жалпы алғанда, 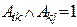орындалатындай к саны бар болса ғана 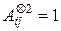болады, басқаша айтқанда υі төбесімен υк төбесін және υк төбесімен υі төбелерін қосатын қабырға бар. Сондықтан υі төбесінен υj төбесіне апаратын ұзындығы 2-ге тең жол бар.

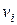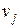Теорема. Айталық, G төбелері υ1, υ2, υ3... υn және сыбайлас А матрицасы берілген бағытталған граф болсын. мен төбелерінің арасында 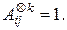(1≤к≤n) шарты орындалса ғана ұзындығы к –ға тең жол бар болады.