Тапсырмалар және әдістемелік ұсыныстар.
1-практикалық сабақ.Жиындардың берілу тәсілдері. Эйлер диаграммасы. Жиындар алгебрасындағы тепе-теңдіктерді дәлелдеу. Жиындар арасындағы әртүрлі сәйкестіктер құру, олардың қасиеттерін үйрену. Жиындардың қуатын анықтау. Саналымды С қуатты жиындар.
1. А={2, 3} , B={3,4,5} жиындары берілген. AÈB, AÇB, A\ B, B\A, A´B, B´A табыңыз. Декарт көбейтіндісіне геометриялық интерпретация беріңіз.
2. A\(BÈC)=(A\B)\C тепе-теңдігін дәлелдеңіз.
3. А={x|2£x£3}, B={y|3£y£5} жиындары берілген. AÈB, AÇB, A\B, B\A табыңыз. Декарт көбейтіндісіне геометриялық интерпретация беріңіз A´B, B´A.
4.Айталық, [0,1], [0,2] сандар осінен алынған кесінділер болсын. [0,1]х[0,2], [0,1]2, [0,2]2 жиындарына геометриялық интерпретация беріңіз.
5. A\(B\C)=(A\B)È(AÇC) тепе-теңдігін дәлелдеңіз.
6. АхВ 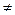 ВхА болатындай А және В жиындарын құрыңыз.
ВхА болатындай А және В жиындарын құрыңыз.
7. 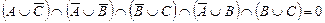 тепе-теңдігін дәлелдеңіз.
тепе-теңдігін дәлелдеңіз.
8. 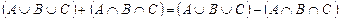 тепе-теңдігін дәлелдеңіз
тепе-теңдігін дәлелдеңіз
9. 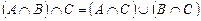 қатынасының дұрыстығын дәлелдеңіз.
қатынасының дұрыстығын дәлелдеңіз.
10.А={a, b} және B={c, d} жиындары берілген. Бұл жиындардың арасында неше әртүрлі сәйкестік орнатуға болады. А-ны В-ға іштей бейнелеу, функционал бейнелеу, функцияларды сипаттаңыз.
11. Айталық, G (х-3)2 +(у-2)2≤1 қатынасын қанағаттандыратын (х, у) нақты сандар жұптарының жиыны. 2,3,4 сандарының образын, прообразын анықтаңыз; [2,3], [2,4] кесінділерінің образы мен прообраздары қандай? G сәйкестігінің қасиеттері?
12. Айталық, G х–2=у қанағаттандыратын түзу сызық нүктелерінің х,у≥0 жиыны; G сәйкестігінің қасиеттері қандай?
13. f(x)=2x және g(x)=1+x функцияларының композициясы неге тең?
14. А={1, 2, 3, 4}жиыны және бұл жиынның 2 түрлендіруі (1→3, 2→3, 3→1, 4→2) және (1→2, 2→1, 3→1, 4→3) берілген. Түрлендірулердің композициясы неге тең?
15. Квадрат пен кесінді нүктелерінің жиындары эквивалентті екенін дәлелдеңіз.
16. Барлық нақты сандардың саналымды тізбектерінің қуаты қандай?
17. Ақырлы жиындардың кез келген ішкі жиыны ақырлы екенін дәлелдеңіз.
18. Ақырлы жиындардың ақырлы санының Декарт көбейтіндісі ақырлы болатынын дәлелдеңіз.
19. Айталық, функцияның анықталу облысы саналымды болсын. Осы функцияның мәндер жиыны ақырлы немесе саналымды болатындығын дәлелдеңіз.
20. Екі шеңбердің нүктелер жиыны эквивалентті екенін дәлелдеңіз.
21. Егер саналымды жиыннан ақырлы ішкі жиын алынып тасталса, қалған жиын саналымды болады. Дәлелдеңіз.
Әдістемелік ұсыныс.Тапсырманы орындау үшін жиындар теориясына оқылған дәріс материалдарын және ұсынылған әдебиеттен жиындармен орындалатын операциялар, Венн диаграммаларымен инъективті,биективті бейнелеу, жиындардың қуаты ,саналымды жиындар, Декарт көбейтіндісі ұғымдарымен танысыңыз және бақылау сұрақтарына жауап беріңіз.
Негізгі әдебиет 3[10-43]
Қосымша әдебиет 7[9-25]
Бақылау сұрақтары
1. Жиындармен негізгі операцияларды атаңыз.
2. Бірігу, қиылысу, толықтауыш операциялардың негізгі қасиеттерін атаңыз.
3. Әр операцияға Эйлер-Венн диаграммаларын сызыңыз.
4. Қандай жиындар тең болады.
5. Қандай сәйкестік бейнелеу деп аталады?
6. Инъективті,биективті бейнелеулерге мысал келтіріңіз.
7. Ағылшын-орыс сөздігі ағылшын және орыс сөздерінің арасында сәйкестік орнатады. Бұл сәйкестік қандай қасиеттерге ие?
8.Қандай жиындар тең болады?
9. Жиындар арасындағы қандай сәйкестік өзара бірмәнді деп аталады?
10. Жазықтықтың нүктелер жиынының қуаты қандай?
11. Рационал сандар жиыны саналымды екендігін дәлелдеңіз
2-практикалық жұмыс.Қатынастар. Бинарлы қатынастардың берілу тәсілдері. Эквивалентті және ретті қатынастар (2-сағ).
1. Р қатынасының анықталу облысын, мәндер жиынын анықтаңыз. Р қатынасын рефлексивті, симметриялы, антисимметриялы, транзитивті деуге бола ма?
Р  R2, P={(x,y)|x2+y2=1}
R2, P={(x,y)|x2+y2=1}
2. Рефлексивті, симметриялы емес, транзитивті бинарлы қатынас құрыңыз.
3. M= {a,b,c}-жиынының булеанында берілген R1және R2 қатынас-тарының матрицаларын құрыңыз. R1=«бос емес қиылысуы бар»;
R2= «қатаң кіреді».
4. {(a,b) | (a-b) рационал сан қатынасы нақты сандар жиынында эквиваленттік қатынас екендігін дәлелдеңіз.
5. M={1,2,3,4,5,6,7,8,9} жиынында төмендегі қатынастар қандай қасиеттермен сипатталады?
а) R1={(a, b):(a-b)–жұп};
б) R2={(a, b):(a+b)–тақ};
в) R3={(a, b):(a +1)–(a+b) бөлгіші};
г) R4={(a, b):a–(a+b), a≠1 бөлгіші} ;
6. M={2, 4, 6} жиынында R-«кіші болу» қатынасы анықталған. Сипат-тамалық қасиетімен және тізіммен R қатынасын, R-1 кері қатынасты және R-ге толықтауыш қатынастарын беріңіз. Қатынастарды салыстырыңыз. Олардың қасиеттерін анықтаңыз.
7. R1, R2 қатынастары N жиынында берілген болсын.
R1={(a,b):b=a+2; a,bÎN};
R2={(a,b):b=a2; a,bÎN}.
R1 ○ R2 , R2 ○ R1, R12, R22 қатынастарын анықтаңыз.
Әдістемелік ұсыныс.Тапсырманы орындау үшін оқылған дәріс материалдары мен ұсынылған әдебиеттен қатынастар, бинарлы, эквивалентті және ретті қатынастар, қатынастардың қасиеттері, кері қатынастар туралы материалдарды оқып бақылау сұрақтарына жауап дайындаңыз.
Негізгі әдебиет 2[12-20]
Қосымша әдебиет 18[48-64]
Бақылау сұрақтары
1.Қатаң ретті қатынастардың қандай қасиеттері бар?
2.Бинарлы қатынасты қалай беруге болады?
3.Қатынастың транзитивті тұйқталуын қалай табуға болады?
4.Кері қатынастың матрицасын алу үшін бинарлы қатынастың матрицасын қалай өзгертуге болады?
3-практикалық жұмыс. Логикалық функциялардың ақиқаттық кестесін құрыңыз. Формулаларды эквивалентті түрлендірулері. Логикалық функцияларды жіктеу. МДҚФ, МКҚФ.
1. F1 және F2 логикалық функциялары үшін ақиқаттық кесте құрыңыз.
F1=(X V Y)®(ZÅX); F2=XYZ®(Z V X).
2. f(x,y,z)=x&yVy&z функциясының маңызды айнымалыларының жиынын көрсетіңіз.
3. X&(X V Z) &(Y V Z) 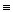 (X&Y) V (X&Z) эквиваленттікті дәлелдеңіз.
(X&Y) V (X&Z) эквиваленттікті дәлелдеңіз.
4. f= 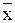
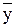 V(x y Å z) функциясының қандай екендігін анықтаңыз. (тепе-тең ақиқат, тепе-тең жалған немесе орындалушы).
V(x y Å z) функциясының қандай екендігін анықтаңыз. (тепе-тең ақиқат, тепе-тең жалған немесе орындалушы).
5. Импликация, 2-ң модулі бойынша қосу, Пирс стрелкасы функ-цияларының ассоциативтігін тексеріңіз.
6. 1-тапсырмадағы F1 және F2 функцияларын ДҚФ, КҚФ түрлендіріңіз. Оларға МДҚФ, МКҚФ табыңыз.
7. f(x,y,z) логикалық функция аргументтерінің мәндер жиынтықтары тізбегімен берілген. Оның мүлтіксіз конъюктивті қалыпты формасын табыңыз (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1):f=( 0 1 1 1 0 1 1 0 ).
8. f(x,y,z)=(xVy)®(xÅz) логикалық функциясының мүлтіксіз дизъюнк-тивті қалыпты формасын табыңыз.
9. f=x&( 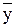 V z) функциясының х айнымалысы бойынша, х және у бойынша және х, у, z бойынша жіктеулерін табу керек.
V z) функциясының х айнымалысы бойынша, х және у бойынша және х, у, z бойынша жіктеулерін табу керек.
10. Эквивалентті түрлендірулердің көмегімен ( 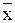 &(уVz))
&(уVz)) 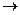 (x&y)Vz формуласын ДҚФ, КҚФ түріне түрлендіру керек.
(x&y)Vz формуласын ДҚФ, КҚФ түріне түрлендіру керек.
11. 2-ң модулі бойынша қосу операциясына МДҚФ анықтаңыз.
Әдістемелік ұсыныс.Тапсырманы орындау үшін оқылған дәріс материалдары мен ұсынылған әдебиеттенлогикалық функциялар, импликация, 2-ң модулі бойынша қосу, Пирс стрелкасы функциялары, логикалық функциялардыдизъюнктивті, конъюнктивтіқалыпты формаларға түрлендіру және әр түрлі әдістермен мүлтіксіз дизъюнктивті қалыпты форма, мүлтіксіз конъюнктивті қалыпты формаларын табу туралы материалдарды оқып бақылау сұрақтарына жауап дайындаңыз.
Негізгі әдебиет 3[172-193], 1[11-17]
Қосымша әдебиет 7[66-80] ,7[50-65]
Бақылау сұрақтары:
1. МДҚФ деген не?
2. МДҚФ әр конъюкциясының рангісі нешеге тең?
3. МКҚФ-ға қандай элементар операциялар кіреді?
4. МКҚФ қанша элементар дизъюнкциялар кіреді?
5. Қандай логикалық функция екінің модулі бойынша қосу опера-циясының терістеуі деп аталады.?
6. Қандай функция тавтология деп аталады?
7. Қандай функция жалған деп аталады?
8. Үшіншіні шығару заңы қандай?
4-практикалық жұмыс.Жегалкин алгебрасы. Логикалық функциялар жүйесін толықтыққа зерттеу.
1. Эквивалентті түрлендірулерді пайдаланып f=( 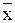 |
| 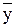 )
) 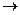 (xyÅz) функ-циясы үшін Жегалкин көпмүшелігін құру керек.
(xyÅz) функ-циясы үшін Жегалкин көпмүшелігін құру керек.
2. Анықталмаған коэффициенттер әдісін пайдаланып XYZ®(Z V X) функциясы үшін Жегалкин көпмүшелігін құру.
3. (х 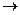
 у) | z функциясы сызықты ма? 2- модулі бойынша қосу және конъюнкция арқылы дизъюнкцияға өрнек табыңыз.
у) | z функциясы сызықты ма? 2- модулі бойынша қосу және конъюнкция арқылы дизъюнкцияға өрнек табыңыз.
4. Дизъюнкцияны 2-нің модулі бойынша қосу және конъюнкция арқылы өрнектеңіз.
5. f=(x®y)Åz функциясы өзіне-өзі түйіндес пе?
6. f=(x V y)®(z Å x) функциясы монотонды ма?
7. {f1,f2} функциялар жүйесі толық па?
f1=xyÅ(y® z). f2= 
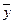 V(x y Å z).
V(x y Å z). 
8. f=x & ( 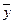 V z) функциясы нольмен бірді сақтай ала ма?
V z) функциясы нольмен бірді сақтай ала ма?
9. { x | y } {x, x ® y} {x + y, x V y, 1} {x V y, x} {x &y, 0, 1 } Логикалық функциялар жүйелерінің қайсысы функционалды толық емес?
Әдістемелік ұсыныс.Тапсырманы орындау үшін оқылған дәріс материалдары мен ұсынылған әдебиеттен,эквивалентті түрлендірулер, анықталмаған коэффициенттер әдістерін пайдаланып Жегалкин көпмүшелігін құру және логикалық функцияларды зерттеу тақырыптарын оқып бақылау сұрақтарына жауап дайындаңыз.
Негізгі әдебиет 1[23-27]
Қосымша әдебиет 3[190-193]
Бақылау сұрақтары:
1.Жегалкин алгебрасына қандай логикалық операциялар кіреді?
2.Қандай функция сызықты?
3.Қандай функция өзіне-өзі түйіндес?
4.Қандай функция монотонды деп аталады?
5-Практикалық сабақ. Комбинаторика. Орналастырулар мен терулер. Жиындарды бөліктеу.(2 сағ)
Таңдаманың немесе бөліктеудің типін анықтап және сәйкес комбинаторикалық формуланы таңдап есепті шығарыңыз.
1. Кітап сөресінде алгебрадан 20 кітап,ықтималдық теориясынан-12, математикалық талдаудан-7 және әдебиеттен-25 кітап бар. Неше әдіспен математикадан кітап таңдауға болады.?
2. Ученик сөзіндегі әріптерден әртүрлі 4 әріптен тұратын неше сөз құрастыруға боладыа?
3. Төрт студент еммтихан тапсырып отыр.Олардың ешқайсысына қанағаттанарлықсыз баға қойылмайтындығы белгілі болса,оларға неше әдіспен баға қоюға болады?
4. Комитетке 9 адам сайланды.Олардың ішінен төраға және оның орынбасарын сайлау керек.Осыны қанша әдіспен жасауға болады.
5.Гүл дүкенінде гүлдің 6 сорты сатылады. Әрқайсысында әр түрлі 10 түс болатындай неше букет жасауға болады?
6. Әр түрлі үш урнаға әртүрлі 10 шарды неше әдіспень орналастыруға болады?
7. Әр түрлі төрт урнаға бірдей 20 неше әдіспен орналастыруға болады?
8. «Спортлото» ( 36 дан 5 номер) ойынында қай жағдайда таңдау дұрыс болады: а) дәл 3 нөмір; б) дәл 4 нөмір; в) дәл 5 нөмір; г) 3 тен кем емес нөмірлерде?
9. 52 картадан тұратын дестеден дәл 10 карта таңдалды. Осылардың ішінде қанша жағдайда а) қарғаның қаншайымы; б) барлық төрт қаншайым; в) барлық карталар бірдей; г)бір де бір тұз жоқ; д) бір ғана тұз; е)ең болмаса бір тұз; ж)дәл екі тұз бар болады.
10. 25 адамнан тұратын топты неше әдіспен 7 коалицияға бөлуге болады: 5 адамнан-2, 7 адамнан -1, 2 адамнан -4?
11. Қытай рестораны 7 тағамның түрінен 3 таңдауға мүмкіндік береді.Неше әдіспен сұраныс жасауға болады ?
12. Ойын сүйектерінің бесеуін лақтырып әртүрлі неше варианттар алуға болады?
13. Жарысқа қатынасушы 17 адамға бірінші, екінші және үшінші орындар берудің неше мүмкіндігі бар?
14. Тақ цифрларды ғана пайдаланып 6000 аспайтын неше төрт орынды сан құруға болады?
15. Роза гүлінің 4 сорты сатылады. 100 розадан неше әртүрлі букет құрастыруға болады?
Негізгі әдебиет 1[130-144]
Қосымша әдебиет 17[190-193]
Бақылау сұрақтары:
1. Қандай таңдамалар теру ,орналастыру деп аталады?
2. n элементов тұратын орналастырулардың саны қанша болады?
3. Тәртіпсіздік санына формула жазыңыз.
4. 2-ші ретті Стирлинга сандарының көмегімен бөліктеудің қандай сандары есептеледі?
№ 6 практикалық сабақ. Графтар. Қасиеттер. Операциялар. Граф сандары. Ағаштар(2 сағ.).
Төбелер жиыны X және G қатынасы бойынша G=G(X) графы мен G оның толықтауышын 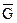 салыңыз.
салыңыз.
G1 графын салыңыз.
G , 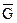 және G1 графтарын салып, олардың инцидентті және сыбайлас матрицаларын құрыңыз.
және G1 графтарын салып, олардың инцидентті және сыбайлас матрицаларын құрыңыз.
G2 графының цикломатикалық саны мен оның тәуелсіз циклдарын сызыңыз.
G3 графының Гранди функциясын құрып, хроматикалық санын табыңыз.
G4 графының ең үлкен толық ішкі графын табыңыз.
G5 графының диаметрін, радиусын және ортасын табыңыз.
8. G6 графының барлық қаңқалы ағаштарын табыңыз.
X={0,1,2,3,4,5}; G:|x-y|>=3; G1=G+K1; G2=G1; G3=G; G4=G1; G5=G1; G6=G1;
1. Кез келген графтың тақ дәрежелі төбелерінің саны жұп болатынын көрсетіңіз.
2. Циклға кіретін кез келген төбенің ілініп тұрмайтындығын көрсетіңіз.
Негізгі әдебиет 1[161-180]
Қосымша әдебиет 19[190-193]
Бақылау сұрақтары:
1.Графтармен операцияларды атаңыз.
2.Графтық цикломатикалық саны нені көрсетеді?
3.Хроматикалық санды қалай табуға болады?
4.Ағаштың қасиеттерін атаңыз.
7-практикалық жұмыс. Графтағы маршруттар. Гамильтон шын-жырлары , циклдары (2 сағ)
1. Сыбайлас матрицасымен берілген графтан шынжыр емес , қарапайым емес шынжыр, қарапайым шынжыр болтын маршруттарды және цикл емес тұйық маршрутты, қарапайым емес цикл , қарапайым циклдарды көрсетіңіз.
2. Егер V={1,2,3,4,5,6}, ал Е={(1,2), (1,4), (2,3), (2,4), (2,5), (3,4), (4,6), (5,6)} болса, онда G(V,E) графынан Эйлер циклын құрыңыз.
3. Сыбайлас матрицасымен берілген графтың мықты байланысқан ком-поненттерін атаңыз.
4. Доғаларының ұзындықтарынан құрылған матрицасы арқылы берілген тиелген бағытталған графта теріс ұзындықтағы қарапайым контурларды анық-таңыз. Бірінші төбеден қалған төбелерге дейінгі жолдардан 6-дан аспайтын доғасы бар ең кіші ұзындықтағы жолдарды табыңыз.

| 
| 
| |||

| 
| 
| -1 | ||

| 
| 
| 
| 
| 
|

| -3 | 
| 
| 
| 
|

| 
| 
| 
|
Негізгі әдебиет 1[180-206]
Қосымша әдебиет 19[190-193]
Бақылау сұрақтары:
1. Қандай маршрут шынжыр, қарапайым шынжыр деп аталады?
2. Цикл, қарапайым циклдар дегеніміз не?
3. Байланысты бағытталмаған графтың екі төбесінің арасындағы ең қысқа жолды анықтайтын Форд алгоритмін атаңыз.
4. Эйлер графы болудың қажетті және жеткілікті шарты қандай?
8-практикалық жұмыс.Транспорт желелерiндегi ағындар.Форд-Фалкерсон алгоритмiн пйдаланып, өткiзу мүмкiндiгi C=(c1, c2 ,c3,…c14) векторымен берiлген транспорт желiсi үшiн ең үлкен ағынды табыңыз.
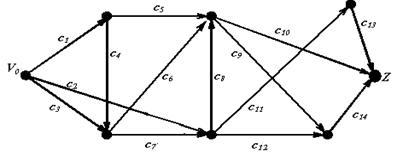
Тапсырмалар варианты.
1. С = (12, 37, 8, 5, 18, 9, 10, 57, 6, 27, 11, 42, 6, 28)
2. С = ( 20, 5, 2,19, 31, 7, 19, 4, 2, 8, 3, 2, 5, 21)
3. С = (1, 44, 35, 21, 61, 1, 31, 2, 4, 1, 5, 32, 82,6)
4. С = ( 27, 14, 35, 71, 4, 1, 1, 13, 21, 16,49, 4, 8, 11)
5. С = ( 3, 7, 12, 8, 24, 9, 13, 5, 4, 2, 16, 3, 6 ,28)
6. С = ( 5, 24, 2, 5, 9, 1, 61, 53,22, 3, 1, 61, 2, 51)
7. С = ( 72, 35, 2, 3, 6, 13, 41, 4, 21, 21, 6, 5, 7, 30)
8. С = ( 5, 41, 2, 49, 25, 2, 1, 3, 39, 7, 10, 21, 3, 22)
9. С = ( 6, 23, 32, 6, 9, 12, 41, 5, 24, 6, 8, 6, 9, 10)
10. С = ( 41, 5, 2, 19, 35, 14, 1, 23, 12, 3, 8, 72, 3, 42)
11. С = ( 6, 32, 81, 4, 6, 21, 41, 74, 58, 3, 1, 20, 7, 14);
12. С = ( 51, 4, 52, 9, 5, 2, 11, 3, 42, 6, 9, 22, 8, 73)
13. С = ( 1, 34, 2, 19, 6, 42, 37, 25, 2, 26, 91, 52, 2, 60)
14. С = (6, 34, 21, 81, 2, 7, 31, 6, 19, 4, 2, 2, 1, 23)
15. С = (6, 34, 21, 81, 2, 7, 31, 6, 19, 4, 2, 2, 1, 30)
16. С = ( 7, 3, 2, 19, 7, 12, 52, 7, 2, 9, 9, 31, 12,14)
17. С = ( 5, 41, 23, 1, 7, 27, 42, 92, 6, 9, 33, 55,4, 17 )
18. С = ( 6, 32, 12, 4, 5, 2, 11, 3, 42, 6, 9, 22, 3, 19)
19. С = ( 7, 32, 2, 31, 9, 2, 17, 9, 3, 56,19, 2, 17, 25)
20. С = ( 8, 16, 47, 2, 61, 6, 21, 7, 2, 42, 45, 2, 4,5)
Негізгі әдебиет 1[249-257]
Қосымша әдебиет 19[190-193]
Бақылау сұрақтары:
1. Қандай орграф транспорттық желі деп аталады?
2. Ағын функциясы ның қандай қасиеттері бар?
3. Қандай доға қаныққан деп аталады.?
4. Қандай ағын толық деп аталады.?
Бақылау жұмыстарының тақырыптары мен нұсқалары (4 бақылау жұмысы ).
1 Бақылау жұмысы.Жиындар теориясы. Сәйкестiктер, бейнелеулер, функциялар. А={a,b,c} және B={1,2,3,4} жиындарының арасында Р сәйкестiгi бар. Р-1 сәйкестiгiн табыңыз. Екi сәйкестiктiң де анықталу облысы мен мәндер жиынын табыңыз. Оларды график түрiнде өрнектеңiз. Сәйкестiктердiң қасиетiн зерттеңiз.
Тапсырма рұсқалары
1. P={(a,1),(a,2),(b,3),(c,2),(c,3),(c,4)}
2. P={(а,3), (a,2), (a,4), (b,1), (c,2), (c,4)(c,3)}
3. P={(a,2),(a,4),(b,1),(b,2),(b,4),(c,2),(c,4)}
4. P={(а,2),(a,4), (a,3), (c,1), (c,2), (c,3)}
5. P={(а,2),(a,4), (a,3), (c,1), (c,2), (c,3)}
6. P={(а,3),(b,4), (b,3), (c,1), (c,2), (c,4)}
7. P={(а,2),(a,3), (a,4), (b,1), (b,2), (b,4)}
8. P={(а,1),(a,2), (b,3), (b,4), (c,3), (c,4)}
9. P={(а,2), (a,3), (a,4), (c,3), (c,1), (c,4)}
10. P={(а,1),(a,2), (a,4), (b,2), (b,4), (c,3)}
11. P={(b,1), (b,3), (c,1), (c,2), (c,3), (c,4)}
12. P={(а,2), (a,4), (b,3), (c,1),(c,2)}
13. P={(а,3), (a,2), (b,2), (b,3), (c,1), (c,4)}
14. P={(а,1), (a,3), (a,4), (b,3), (c,1), (c,4)}
15. P={(а,1), (b,3), (c,1), (c,4), (c,3), (c,2)}
16 .P={(а,1), (b,3), (b,1), (b,4), (c,3), (c,2)}
17. P={(а,1), (а,2), (a,4), (b,1), (b,4), (c,3)}
18. P={(а,1), (а,4), (b,2), (b,3), (c,1), (c,4)}
19. P={(а,1), (а,2), (b,2), (b,4), (c,3), (c,2)}
20. P={(a,1), (a,2), (a,4), (c,3), (c,2), (c,4)}
б)Айнымалылардың барлық мүмкiн мәндерiнде мәнi берiлген функциясы үшiн МДҚФ,МКҚФ табыңыз.
Тапсырма варианттары
1. f(x, y, z, t) = (0011100011001100)
2. f(x, y, z, t) = (1011011000110100)
3. f(x, y, z, t) = (1001010011100101)
4. f(x, y, z, t) = (0011011011011010)
5. f(x, y, z, t) = (1001000100101100)
6. f(x, y, z, t) = (1010011001001011)
7. f(x, y, z, t) = (1001100010011100)
8. f(x, y, z, t) = (0100100010011100)
9. f(x, y, z, t) = (1101001110010010)
10. f(x, y, z, t)= (1011001110001010)
11. f(x, y, z, t) = (1110001101010010)
12. f(x, y, z, t) = (1000101001111010)
13. f(x, y, z, t) = (1100101001101000)
14. f(x, y, z, t) = (1010001110010100)
15. f(x, y, z, t) = (0111011010101001)
16. f(x, y, z, t) = (1011101001011001)
17. f(x, y, z, t) = (1100011101001110)
18. f(x, y, z, t) = (1001000011110101)
19. f(x, y, z, t) = (0100110100101011)
20. f(x, y, z, t) = (0110101101000110)
в)Жегалкин алгебрасы. f(x, y, z) функциясы үшiн Жегалкин полиномын табыңыз.
Тапсырма варианттары:
1. f(x, y,z ) = ( x Ú y) ¯ (y® 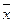 )(xÅ
)(xÅ 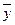 )® (z |
)® (z |  ).
).
2. f(x, y,z ) = (x ¯ ( 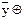 (
( 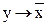 ))( x Ú (
))( x Ú ( 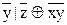 ) )).
) )).
3. f(x, y,z ) = x® (y ¯ z) ↔ (x®y) ¯(x®z).
4. f(x, y,z ) =  .
.
5. f(x, y,z ) = (x Ù y)«(y¯ 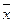 )(x®
)(x® 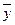 )|(z Å
)|(z Å  ).
).
6. f(x, y,z ) = x«(y Å z) 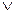 (x«y) Å (x«z).
(x«y) Å (x«z).
7. f(x, y,z ) = 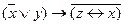 .
.
8. f(x, y,z ) = (x Å y)|(y¯ 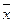 )↓(x «
)↓(x « 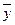 ) ®(z
) ®(z  ).
).
9. f(x, y,z ) = x ¯(y Å z) | (x ¯ y) Å (x ¯ z).
10. f(x, y,z ) = 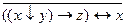 .
.
11. f(x, y,z ) = x Å( 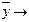
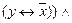
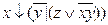
12. f(x, y,z ) = x Ú (y Å z) → (x Ú y) Å (x Ú z)
13. f(x, y,z ) = 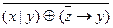 .
.
14. f(x, y,z ) = (x|y)®(y Å 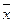 )(x Ù
)(x Ù 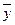 ) (z «
) (z « 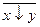 ).
).
15. f(x, y,z ) = x® (y|z) Å (x® y) | (x®z).
16. f(x, y,z ) = 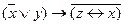 .
.
17. f(x, y,z ) = 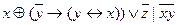 .
.
18. f(x, y,z ) = x ¯ (y«z) Å (x ¯ y) « (x ¯ z).
19. f(x, y,z ) = 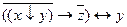 .
.
20. f(x, y,z ) = x Ú (y«z) Å (x Ú y) « (x Ú z).
2. Бақылау жұмысы. Логикалық функциялардың толық жүйелері. Комбинаторика.
а) f1 және f2 функцияларының қандай класқа жататындығын анықтаңыз. Пост теоремасына сүйенiп
{ f1 ,f2 } функциялар жүйесiнiң толықтығын тексерiңiз.
| № | Тапсырмалар нұсқалары | № | Тапсырмалар нұсқалары | № | Тапсырмалар нұсқалары |
| F1=(0 1 0 1 1 0 1 1) f2=(x V y)®(z Å x) | f1=(0 1 1 0 1 1 1 0) f2=x Å y V z | f1=(0 1 1 1 1 1 0 1) f2=(x V y)® xyz | |||
F1=(0 1 0 1 1 0 0 1)
f2=(x ® y) V 
| f1=(0 1 1 0 0 0 1 1) f2=(x Å y)®(y V x) | f1=(1 0 0 1 0 1 0 0) f2=(x V y)®(z Å x) | |||
f1=(0 1 0 1 0 1 1 0)
f2=x & ( 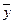 V z) V z)
| f1=(0 1 1 0 1 1 0 1) f2=(x Å z)®(xVy) | f1=(1 0 0 1 1 0 0 1) f2=(x ® y) & z | |||
f1=(0 1 0 1 0 0 1 1)
f2=(x ® 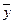 ) Å z ) Å z
| f1=(0 1 1 1 0 1 0 0) f2=x&y Å z&x | f1=(1 0 0 1 0 1 1 0) f2=x V yz | |||
F1=(0 1 0 1 1 1 0 1)
f2=x y V z (x Å 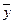 ) )
| f1=(0 1 1 1 1 0 0 1)
f2=  yz®(zVx) yz®(zVx)
| f1=(1 0 0 1 0 0 1 1) f2=(x ® y) Å z | |||
| f1=(0 1 1 0 0 1 0 0) f2=x y Å (y ® z) | f1=(0 1 1 1 0 1 1 0) f2=(x®y)Å(zÅy) | f1=(1 0 0 1 1 1 0 1) f2=xy V z(x Å y) | |||
f1=(0 1 1 0 1 0 0 1)
f2=  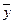 V(x y Å z) V(x y Å z) 
| f1=(0 1 1 1 0 0 1 1) f2=(x V y) Å (z V y) | f1=(0 1 0 1 0 1 1 0)
f2=x & ( 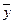 V z) V z)
|
б) Берiлген А цифрлар жиынын пайдаланып қанша әртүрлi үш таңбалы натурал сан алуға болады, егер 1) Әр цифр бiрден артық пайдаланылмайды;
2) Бiр цифрды бiрнеше рет пайдалануға болады;
б) Тапсырма варианттары
| 1.А={3,4,5,6} | 5.А={2,3,5,7,9} | 9.А={2,5,7,8,9} | 13. А={3,4,7,9} | 17. А={2,4,7} |
| 2.А={1,3,5,7} | 6.А={1,4,8,9} | 10.А={3,4,7,8,9} | 14. А={2,5,7,8} | 18. А={1,3,5,8,9} |
| 3.А={2,5,6,7,8} | 7.А={2,3,4,5} | 11.А={1,2,5,6} | 15. А={1,3,4} | 19. А={3,4,7,9} |
| 4. А={3,4,5,9} | 8.А={3,7,8,9} | 12.А={2,3,4,5,6} | 16. А={3,5,7,8,9} | 20. А={2,5,6,7,8} |
в) Тапсырма варианттары
1. 5 кiтапты сөреге қанша әдiспен орналастыруға болады
2. Серванттың бiр қатарына 6 бокалды қанша әдiспен орналастыруға болады.
3. Столға 8 адамнан тұратын президиумды қанша әдiспен отырғызуға болады?
4. 7 адамды қанша әдiспен сапқа тұрғызуға болады?
5. Класқа 10 партаны қанша әдiспен қоюға болады?
6. А,Б,В,Г,Д әрiптерiнен тұратын тiзбектi қанша әдiспен құруға болады?
7. «Персик» сөзiнен қанша әртүрлi 6 әрiптiк тiзбектер алуға болады?
8. 5 пәннен тұратын оқу кестесiн бiр күнге неше тәсiлмен құруға болады?
9. Дастарханға 4 адамды қанша әдiспен отырғызуға болады?
10. Әртүрлi 7 карточка салынған қорапты қанша әдiспен араластыруға болады?
11. Ұсынылған 6 пәннен 3 пәндi неше әдiспен таңдауға болады?
12. Қолда бар 7 түрлi жемiстiң екеуiн қанша әдiспен таңдауға болады?
13. 10 адамнан жиналысқа баратын 3 адамды қанша әдiспен таңдауға болады?
14. Конкурсқа 7 притенденттен 4 студенттi қанша әдiспен таңдауға болады?
15. Сөреде тұрған 10 кiтаптан неше әдiспен оқуға 3 кiтап таңдауға болады?
16. 10 фильмнен тұратын видеотекадан неше әдiспен әртүрлi 4 фильм таңдауға болады?
17. Шкафта iлулi тұрған 8 галстуктен неше әдiспен әртүрлi 2 галстук таңдауға болады?
18. Сатылымдағы 9 түрлi газеттен неше әдiспен әртүрлi 5 газет сатып алуға болады?
19. 8 адамнан тұратын топтан неше әдiспен программалау курсына 3 адам таңдауға болады?
20. Менюде бар 7 тағамнан неше әдiспен 3 түрлi тағам таңдауға болады?
Тапсырмалар варианттары
1. Темiр жол бекетiнде m бағдаршам бар. Егер бағдаршам «қызыл», «жасыл», «сары» 3 күйде болса, олардан неше түрлi сигналдардың комбинациясын беруге болады?
2. Бiр мемлекетте тiстерiнiң жиынтығы бiрдей 2 тұрғын болмаптыегер адамның тiстерiнiң саны 32 десек бұл мемлекеттiң тұрғындарының ең көп саны қанша болуы мүмкiн?
3. Қайталап пайдалануға болатын тақ цифрлардан неше түрлi 4 таңбалы сан құрастыруға болады?
4. Әртүрлi 12 оқу құралын 4 студентке неше әдiспен бәлiп беруге болады?
5. 9 түрлi күмiс ақшаны 2 қалтаға неше түрлi әдiспен салуға болады?
6. Үшеуi ток импульсi , екеуi үзiлiсте болатын әрiптегi 5 түрлi сигналдан алфавиттiң неше әрiбiн құрауға болады?
7. «Статистика», «Парабола» сөздерiндегi әртүрлi алмастырулардың санын анықтаңыз.
8. Апада 2 алма, 3 алмұрт және 4 апельсин бар. Олардан 9 күн бойы баласына бiр талдан берiп отырады. Қанша әдiспен берiп отыруға болады?
9. Почта бөлiмшесiнде 9 түрлi ашық хат сатылады. Ашық хаттың әр түрiнiң саны 8ден кем болмаса 8 ашық хаттан тұратын жиынтықты неше әдiспен сатып алуға болады?
10. 3 жiгiт пен 2 қыз жұмыс орнын iздейдi. Егер қалада 3 тек жiгiттер дi қабылдайтын құю цехтары бар 3 зауыт, қыздарды қабылдайтын 2 тоқыма фабрикасы және жiгiттердi де, қыздарды да қабылдайтын 2 фабрика болса неше әдiспен жұмыс таңдауға болады?
11. Бес қызметкерден тұратын топқа 3жолдама бөлiндi. Жолдамалар әртүрлi болса, оны неше әдiспен үлестiруге болады?
12. Взводта 3 сержант және 30солдат бар. Қарауылға 1 сержант пен 3 солдатты неше әдiспен жiберуге болады?
13. Неше әдiспен 15 студенттi 3 оқу тобына бесеуден бөлуге болады?
14. Жарысқа қатысушы 17 спортшыға бiрiншi, екiншi және үшiншi орындарды неше әдiспен бөлудiң мүмкiндiгi бар?
15. 5әйел және 7 ер адамнан тұратын қазылар алқасы 8 әйел және 11 ер адамнан тұратын тiзiмнен таңдалуы тиiс. Құрамы неше түрлi қазылар алқасын таңдауға болады?
16. Раушангүлiнiң 4 сорты сатылады. Қанша әртүрлi букет құруға болады?
17. Бiрдей 20шарды. Әртүрлi 4 урнаға неше әдiспен салуға болады?
18. Әртүрлi 10 шарды, 3 урнаға қанша әдiспен орналастыруға болады?
19. Белгiлi әртүрлi 7 аттан 4 күшiкке неше әдiспен ат беруге болады?
20. 25 адамнан тұратын топты 7 коалицияға неше әдiспен бөлуге болады:5адамнан 2 коалиция, 7 адамнан 1 коалиция, 2 адамнан 4 коалиция;
д)Жиындарды бөлiктеу. n объектен тұратын жиынды m бос емес бөлiктерге бөлуге болады?
Тапсырма варианттары:
| 1. n =7, m =3 | 5. n =7, m =4 | 9. n =7, m =2 | 13. n =5, m =4 | 17. n =5, m =3 |
| 2. n =4, m =2 | 6. n =7, m =4 | 10. n =8, m =3 | 14. n =6, m =2 | 18. n =5, m =3 |
| 3. n =8, m =6 | 7. n =8, m =2 | 11. n =5, m =3 | 15. n =5, m =2 | 19. n =5, m =3 |
| 4. n =7, m =5 | 8. n =4, m =3 | 12. n =6, m =4 | 16. n =6, m =3 | 20. n =6, m =5 |
3-Бақылау жұмысы.Ең кіші қосылу туралы есеп.
7 төбелі бағытталмаған толық графтың қабырғалар салмағының матрицасы берілген. Оң ең кіші қаңқалы ағашын табыңыз. Жеткілікті түсініктемелермен оны графикалық түрде кескіндеңіз.
Тапсырма варианттары.
| 1. | ∞ | 2. | ∞ | ||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| ∞ | 4. | ∞ | |||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| 5. | ∞ | 6. | ∞ | ||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| 7. | ∞ | 8. | ∞ | ||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| 9. | ∞ | ∞ | |||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| 11. | ∞ | ∞ | |||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| ∞ | 14. | ∞ | |||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| ∞ | 16. | ∞ | |||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
| 20. | ∞ | 21. | ∞ | ||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ | ||||||||||||||
| ∞ | ∞ |
4-Бақылау жұмысы. Ең қысқа жол туралы есеп.
Байланысты тиелген бағытталмаған графта қабырғаларының салмағы L=(l1 ,l2...,l13) түрінде берілген. V0 мен V7 төбелерінің арасындағы ең қысқа жолды табыңыз.
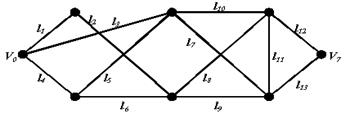
Тапсырмалар варианттары.
1. L = ( 3, 7, 12, 8, 24, 9, 13, 5, 4, 2, 16, 3, 6 )
2. L = ( 5, 41, 23, 1, 7, 27, 42, 92, 6, 9, 33, 55,4 )
3. L = ( 51, 4, 52, 9, 5, 2, 11, 3, 42, 6, 9, 22, 8)
4. L = ( 5, 41, 2, 49, 25, 2, 1, 3, 39, 7, 10, 21, 3)
5. L = ( 7, 3, 2, 19, 7, 12, 52, 7, 2, 9, 9, 31, 12)
6. L = ( 27, 14, 35, 71, 4, 1, 1, 13, 21, 16,49, 4, 8)
7. L = ( 6, 32, 12, 4, 5, 2, 11, 3, 42, 6, 9, 22, 3)
8. L = ( 41, 5, 2, 19, 35, 14, 1, 23, 12, 3, 8, 72, 3)
9. L = ( 72, 35, 2, 3, 6, 13, 41, 4, 21, 21, 6, 5, 7)
10. L = ( 1, 7, 5, 1, 8, 4, 7, 12, 4, 8, 6, 24, 3)
11. L = ( 1, 44, 35, 21, 61, 1, 31, 2, 4, 1, 5, 32, 82)
12. L = ( 7, 32, 2, 31, 9, 2, 17, 9, 3, 56,19, 2, 17)
13. L = ( 6, 23, 32, 6, 9, 12, 41, 5, 24, 6, 8, 6, 9)
14. L = ( 5, 24, 2, 5, 9, 1, 61, 53,22, 3, 1, 61, 2)
15. L = (6, 34, 21, 81, 2, 7, 31, 6, 19, 4, 2, 2, 1)
16. L = ( 20, 5, 2,19, 31, 7, 19, 4, 2, 8, 3, 2, 5)
17. L = ( 8, 16, 47, 2, 61, 6, 21, 7, 2, 42, 45, 2, 4)
18. L = ( 6, 32, 81, 4, 6, 21, 41, 74, 58, 3, 1, 20, 7)
19. L = ( 10, 5, 12, 7, 93, 1, 10, 4, 6, 34, 8, 13, 6)
20. L = ( 1, 34, 2, 19, 6, 42, 37, 25, 2, 26, 91, 52,
Дата добавления: 2015-08-14; просмотров: 5173;
