Электрическая емкость

Электрическая емкость определяется как коэффициент про­порциональности между зарядом, сообщаемым телу, и потенциалом поля на его поверхности:

где С — электрическая емкость. Потенциал поля на бесконечно­сти считаем равным нулю.

Единицей емкости служит фарад — емкость такого тела, по­тенциал поля которого изменяется на 1 В при сообщении ему за­ряда 1 Кл.

Пример. Вычислим электрическую емкость сферы радиусом R, находящейся в вакууме.

Потенциал на поверхности сферы найдем из формулы (10):

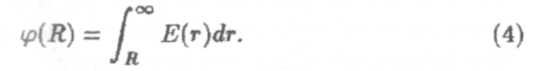
Ранее по теореме Гаусса была получена напряженность электри­ческого поля вне и на поверхности равномерно заряженной сферы (см. лекцию (2), формулу (7)):

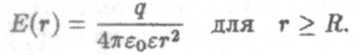
Подставив это выражение в формулу (4), и произведя интегрирование, имеем

Из сравнения (5) и (3) получаем электрическую емкость сферы радиусом R

Заметим, что 4πε₀ имеет порядок 10^_10Ф/м, ε ~ 1, следовательно, емкость в один фарад очень большая величина, так как она соот­ветствует сфере радиусом порядка 10¹⁰ метров. Для сравнения: средний радиус Земли только около 6,4 ∙ 10⁶ м.

Емкость уединенного проводника зависит от диэлектриче­ских свойств окружающей среды. Для однородной, изотропной среды емкость проводника пропорциональна относительной ди­электрической проницаемости среды. Из формулы (6) для сферы имеем

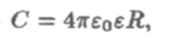
где ε — относительная диэлектрическая проницаемость среды, окружающей сферу.

Система двух проводников, разноименно заряженных равны­ми по абсолютной величине и противоположными по знаку за­рядами, называется конденсатором, если форма и расположение проводников обеспечивают сосредоточение электростатическо­го поля, созданного проводниками, в ограниченной области про­странства. Сами проводники называются в этом случае обклад­ками конденсатора.

Емкостью конденсатора называют отношение заряда, сооб­щаемого конденсатору, к разности потенциалов на его обкладках:

Как мы видели ранее, в плоском конденсаторе

где d — расстояние между обкладками. Из теоремы Гаусса мы получим, что напряженность электростатического поля отлична от нуля только в пространстве между обкладками и равна

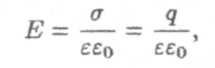
где σ — поверхностная плотность электрического заряда на об­кладках, q — абсолютная величина электрического заряда на каждой из обкладок, S — площадь обкладки. Следовательно, (7) примем в вид:

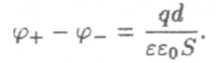
Из (3) получим емкость плоского конденсатора:

где ε — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами.