Генерація другого виміру

Для того, щоб краще зрозуміти фізичну картину утворення двомірного спектру, перш за все згадаємо, що відбувається під час детектування сигналу спаду вільної індукції і яким чином отримується одномірний спектр. Процес детектування включає ідентифікацію компонентів коливань спаду вільної індукції шляхом їх оцифровування через обрані інтервали часу, які для заданого часу збору даних повинні відповідати критерію Найквіста. Накопичений у такий спосіб масив даних, є залежністю інтенсивності сигналу СВІ від часу. Шляхом Фур'є-перетворення ці дані трансформуються в спектр, що являє собою залежність інтенсивності сигналу від частоти. Таким чином, загальна процедура формування частотного виміру полягає у фіксації інтенсивності сигналу через задані інтервали часу. Сукупність таких даних дає інтерферограму, або СВІ. Яким би методом ми не отримали СВІ, його можна перетворити на відповідний спектр ЯМР шляхом Фур'є-перетворення. Цю ідею можна поширити на два частотних виміри. У цьому випадку спектр повинен являти собою залежність інтенсивності сигналу від двох частот, f₁і f₂. Для його одержання необхідно зафіксувати залежність інтенсивності сигналу від двох незалежних часів t₁ і t₂, тобто отримати двомірний масив даних. Кожний рядок такого масиву є функцією t₁, а кожна колонка – функцією t₂. Зрозуміло, що один часовий інтервал і, відповідно, один частотний вимір відповідає звичайному періоду детектування (t₂ на Рис. 5.1). Однак звідки береться другий вимір? Відповідь на це питання і є ключем до розуміння принципів двомірної спектроскопії ЯМР.

Незалежно від природи параметру, що вивчається методом двомірної спектроскопії, всі імпульсні послідовності двомірних методик включають 4 етапи. Вони називаються: підготовчий період, період еволюції, період змішування і період детектування (Рис. 5.1).

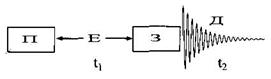
Рис.5.1. Загальна схема будь-якого двомірного експерименту. П: Підготовка, E: Еволюція, З: Змішування й Д: Детектування.

Підготовчий період, як правило, включає релаксаційний проміжок, необхідний для переходу спінової системи у стаціонарний стан, який закінчується збуджуючим імпульсом. Період змішування найчастіше включає імпульс або групу імпульсів і/або фіксовані часові інтервали. Він служить для перерозподілу намагніченості між спіновими станами. У деталях, залежно від типу експерименту, ці періоди можуть суттєво розрізнятися. Період детектування є цілком аналогічним відповідному періоду в одномірних одноімпульсних спектрах. Під час цього періоду відбувається оцифровування сигналу та запис СВІ збуджених спінів. Період еволюції є ключовим для формування другого виміру. Він являє собою проміжок часу, на протязі якого збуджена спінова система набуває необхідних для експерименту властивостей. Особливістю періоду еволюції у двомірній спектроскопії є те, що його тривалість є змінною. Стан, що набуває система у період еволюції впливає на вигляд сигналу СВІ, що утворюється в період детектування.

Розглянемо просту імпульсну послідовність, у якій як підготовчий період, так і період змішування містять лише по одному 90^о_х імпульсу (Рис. 5.2). Ці імпульси розділяє період еволюції, час якого позначимо t₁.

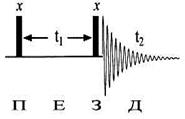
Рис.5.2. Ілюстративна двомірна послідовність, у якій П і З. є 90° імпульсом. Це - базова послідовність COSY.

Нехай послідовність впливає на зразок, молекули якого містять єдиний протон, наприклад, це може бути хлороформ. Будемо вважати, що хімічний зсув зразка дорівнює n Гц. Відповідно до векторної моделі (Рис. 5.3), початковий 90^о_х імпульс перевертає рівноважну намагніченість у площину х-у і розташовує її уздовж осі +у. Після цього вектор намагніченості прецесує (еволюціонує) відповідно до величини його хімічного зсуву n. У системі координат, що обертається, через час t₁ (тривалість періоду еволюції) вектор повернеться на кут 360nt₁ градусів. У цей момент на нього впливає другий імпульс. Для розуміння результату впливу другого імпульсу припустимо, що вектор намагніченості складається із двох ортогональних компонентів. Одна з них спрямована уздовж осі у, її величина становить М_оcos360nt₁. Інша компонента розташовується уздовж осі х і дорівнює М_оsin360nt₁. Другий 90^о_х імпульс розташовує у-компоненту уздовж осі –z. При цьому х-компонента не змінюється і продовжує прецесувати у площині х-у. Цей компонент продукує сигнал СВІ. Фур'є перетворення даного СВІ дає спектр із єдиною лінією, інтенсивність якої визначається фактором 360nt₁. Ця ситуація відрізняється від звичайного одномірного експерименту тим, що другий імпульс виводить частину намагніченості з поперечної площини, тому інтенсивність сигналу, який можна отримати після Фур’є-перетворення залежить від періоду t₁.

Виконання даного експерименту з t₁ = 0 приведе до додавання двох 90^о_х імпульсів, що еквівалентно дії 180^о_х імпульсу. Такий імпульс просто інвертує вихідну намагніченість. Оскільки в цьому випадку не виникає поперечної намагніченості сигнал після Фур'є-перетворення буде містити тільки шуми.

Рис.5.3. Дія послідовності COSY, рис. 5.2, на одиничний, сигнал, що не має спінового зв'язку

Рис.5.3. Дія послідовності COSY, рис. 5.2, на одиничний, сигнал, що не має спінового зв'язку

Тепер уявімо собі, що буде відбуватися, якщо повторювати експеримент, даючи фіксовані прирости інтервалу t₁. Результат будемо записувати окремо для кожного варіанта t₁. Оскільки t₁ зростає від нуля, інтенсивність сигналу в результуючому спектрі також буде зростати від нуля. Вона досягне максимуму при 360nt₁ = 90^о. Після чого починається її спад. При подальшому зростанні тривалості інтервалу t₁ Вона доходить до нуля, стає негативною й починає знову зростати. Таким чином, вона змінюється за синусоїдальним законом. Можна сказати, що амплітуда сигналу є модульованою синусоїдальною функцією. Якщо кожний, отриманий у такий спосіб сигнал СВІ (він є функцією t₂) піддати Фур'є-перетворенню, одержимо серію спектрів з єдиним сигналом, інтенсивність якого буде функцією від 360nt₁ (Рис. 5.4).

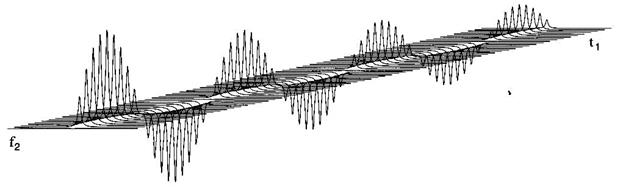
Рис.5.4. Модуляція амплітуди резонансу синглету як функція періоду еволюції t₁. При зростанні t₁ інтенсивність сигналу зменшується через спінову релаксацію

На Рис. 5.4. такі спектри намальовано один за одним під деяким кутом до спостерігача. При великих t₂ релаксаційні ефекти зменшують величину намагніченості відповідно до часу поперечної релаксації Т₂*, тому на додаток до амплітудної модуляції, для сигналу характерний постійний експоненціальний спад. Якщо з кожного спектру взяти лише одну точку, що відповідає максимуму сигналу, то отримаємо масив даних, що нічим не відрізняється від СВІ, за винятком способу його отримання. Таким чином, інтенсивність сигналу відносно t₁ змінюється ідентично сигналу спаду вільної індукції. Такий СВІ був отриманий непрямим методом (Рис. 5.5).

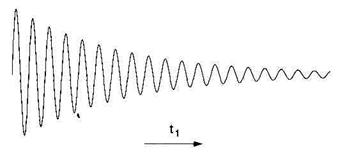
Рис. 5.5. Зміна пікової інтенсивності амплітудно модульованого сигналу, рис. 5.4, дає СВІ (інтерферограму) для виміру t₁.

Частота амплітудної модуляції відповідає хімічному зсуву сигналу в системі координат, що обертається. Говорять, що намагніченість є поміченою частотою n відносно t₁. Якщо піддати цю часову залежність Фур'є перетворенню, одержимо резонансний сигнал з хімічним зсувом n Гц у вимірі f₁, цілком аналогічно до того, як і у вимірі f₂.

У наведеному вище прикладі ми заздалегідь знали, що потрібно слідкувати за інтенсивністю сигналу у точці що відповідає частоті його поглинання. У реальних спектрах частоти поглинання сигналів є цілком довільними. Тому для формування непрямого виміру доводиться слідкувати за інтенсивністю сигналів у всіх точках спектру з певними проміжками між ними і для кожного варіанту виконувати Фур’є-перетворення. Таким чином, для побудови двомірного спектру проводиться моніторинг інтенсивності кожної точки даних у вимірі f₂ як функції t₁. У цьому випадку одержимо повний двомірний набір даних. Наступні Фур'є-перетворення відносно t₁ формують новий частотний вимір, що у сукупності із частотним виміром f₁ дає двомірний спектр. У такому спектрі в обох вимірах присутній єдиний сигнал із частотою n Гц (Рис.5.6).

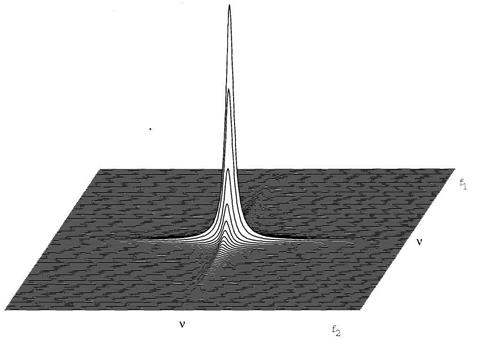
Рис. 5.6. Двомірний спектр, отриманий за допомогою послідовності, що наведена на рис. 5.2, для зразка, який містить єдиний спін, що не має спінового зв'язку. Пік має зсув ν Гц в обох вимірах

Відзначимо, що позначення частотних осей як f₁ і f₂ випливає з порядку відповідних часових інтервалів в імпульсній послідовності. Воно визначається тим, що інтервал t₂ знаходиться після інтервалу t₁. Новий уявний (t₁) часовий вимір утворюється точка за точкою шляхом вимірювання сигналу СВІ для кожного значення t₁ (Рис. 5.7) і роздільного запису цих СВІ в пям”яті комп’ютера.

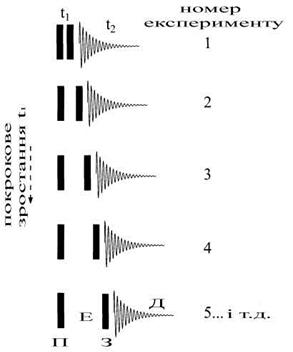
Рис 5.7. Узагальнена схема збору двомірних наборів даних. Експеримент повторюється багато разів з покроковим збільшенням періоду t₁. Отримані СВІ, запам'ятовуються окремо. Наступне подвійне Фур'є-перетворення відносно t₂ і потім t₁, приводить до одержання двомірного спектру.

Таким чином, отримуємо серію СВІ, кожний з яких записаний для певного t₁ (в одномірному спектрі записуються точки одного СВІ як функція t₂). Цей підхід є загальним для будь-яких двомірних експериментів. Дана ідея може бути поширеною на три і більше вимірів. Так, імпульсна послідовність для одержання тримірного спектру містить три часових інтервали. Для одержання такого спектру один вимір детектується прямо, а два – опосередковано (Рис. 5.8).

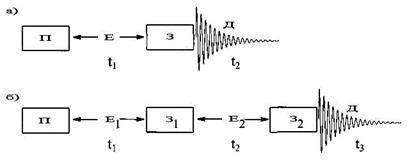
Рис.5.8. Схема (a) двомірних і (б) тримірних експериментів. Накопичення даних в 3D експерименті відбувається при варіюванні незалежних змінних інтервалів t₁ і t₂. У результаті, за аналогією із двомірним експериментом, виникають незалежні виміри f₁ і f₂ .