Правила спін-спінової взаємодії 1-го порядку

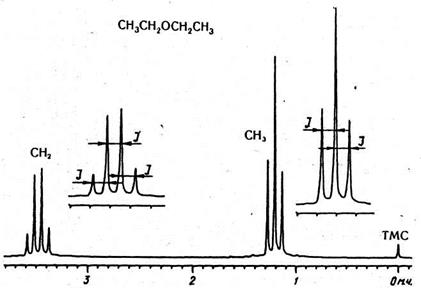
У спектрах ЯМР часто трапляється, що сигнали окремих магнітних ядер або груп еквівалентних ядер містять декілька спектральних ліній. Таке розщеплення називають надтонкою структурою спектра. Отже, сигнал може мати вигляд як одиночного піку (синглет), так і подвоєного (дублет), потроєного (триплет) та більш складних піків, які у загальному випадку називають мультиплетами. Так, протонний спектр діетилового ефіру, що виміряний на частоті 100 МГц, містить триплет і квартет (рис. 1.22).

Рис. 1.22. Спектр діетилового ефіру на ядрах ¹Н. Вигляд мультиплетів показано у збільшеному вигляді. Відстань між компонентами мультиплетів дорівнює константі спін-спінової взаємодії J.

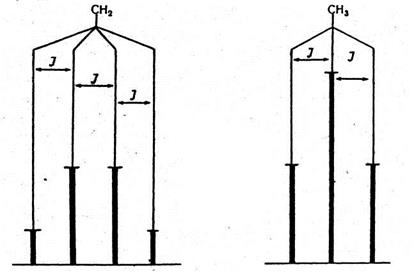
Рис. 1.23. Вигляд розрахованих мультиплетів для спінової системи діетилового ефіру

Сигнали, що відповідають усім магнітно-нееквівалентним протонам сполуки, роз­щеплюються на мультиплети—триплет (СН₃) і квартет (СН₂). Надтонка структура сигналів зумовлена явищем, яке відоме під назвою спін-спінової взаємодії (coupling). Відстань між двома сусідніми компонентами у кожно­му з мультиплетів, виражена в герцах, називається константою спін-спінової взаємодії (КССВ, coupling constant, J). На відміну від хімічного зсуву, КССВ не залежить від робочої частоти приладу, тому відстань між компонентами мультиплетів є однаковою, незалежно від приладу, на якому виміряний спектр. У наведеному прикладі наявне розщеплення можна зобразити схемою, що наведена на рис. 1.23.

Причину виникнення спін-спінової взаємодії розглянемо на прикладі найпростішої молекули з нееквівалентними магнітними ядрами Н—D. Якщо якимось чином поле магнітного моменту протона передається на дейтрон, то напруженість магнітного поля, при якій дейтрон прецесує у постійному магнітному полі, залежить від магнітного квантового числа певного протона. Нехай це число дорівнює + 1/2, тобто вектор магнітного моменту протона орієнтується за полем. Тоді сумарне магнітне поле, що діє на дейтрон, складатиметься з прикладеного зовнішнього магнітного по­ля Н_оі поля ΔH, наведеного протоном. Отже, для досягнення резонансної частоти дейтрона в молекулі Н—D потрібна нижча напруженість магнітного поля H₀ ніж у випадку вільного атома дейтерію. У молекулі, в якій протон має магнітне квантове чис­ло -1/2, наведене ним магнітне поле є протилежним до зовнішнього магнітного поля H_о, і тому необхідне для резонансу дейтрона магнітне по­ле буде вищим, ніж для вільного атома дейтерію. Отже, спектр на частоті дейтерію буде містити дві компоненти (рис. 1.24, зліва). Інтенсивності обох компонентів однакові, оскільки ймовірності того, що протони матимуть магнітне квантове число +1/2 і -1/2, практично однакові.

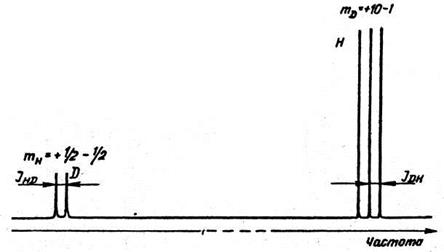Рис. 1.24. Схематичне зображення спектра ЯМР молекули НD: зліва – на частоті дейтерію, справа – на частоті протонів.

На рис. 1.24 (справа) показано інший спектр Н—D, тепер вже на частоті протона. Тут сигнал розщеплюється на три компоненти однакової інтенсив­ності, оскільки спін дейтрона, який зумовлює це розщеплення, дорівнює 1, і відповідно його магнітне квантове число може мати три значення:-1,0 і +1. Зазначимо, що КССВ J_HDта J_DHмають однакові значення (43 Гц), тобто розщеплення як протонного, так і дейтронного сигналів відбуваються з одна­ковою константою.

У загальному випадку, кількість компонентів у спінових мультиплетах можна визначити за формулою

n_A = 2SS_B + 1 (1.18)

де n — мультиплетність сигналу магнітних ядер А; ∑S_В — сума спінів сусідніх еквівалентних ядер В. Для випадку спектрів на ядрах ¹Н, ¹³С та інших, що мають спін 1/2, мультиплетність сигналу можна знайти за формулою

n_A = SN_B + 1 (1.19)

де N_В—кількість еквівалентних ядер у сусідніх групах.

Відносні інтенсивності компонентів мультиплету ядра А визначаються кількістю еквівалентних спінових станів у сусідній групі В. Так, якщо поряд з протоном Н_А знаходиться метильна група

то для протонів метилу можливі орієнтації спінів, наведені на рис. 1.25.

Рис. 1.25. Можливі сполучення орієнтацій спінів протонів метильної групи та їх сумарний спін

Кож­на з восьми комбінацій спінів практично рівноймовірна, однак, у цілому су­марний спін +1/2 або -1/2 дістаємо у результаті трьох різних комбінацій спінових орієнтацій, а сумарний спін +3/2 та -3/2 — лише в одній комбінації. Тому співвідношення інтенсивностей компонентів квартету протона А становить 1:3:3:1.

Якщо біля даного магнітного ядра перебувають дві різні групи еквівалентних протонів В1 і В2, взаємодія з кожною з них іде незалежно. Отже, кількість компонентів у мультиплеті сигналу ядра А буде дорівнювати:

n_A = (2SS_B1 + 1)(2SS_B2 + 1) (1.20)

Де ∑S_B1 та ∑S_В2—відповідно суми спінів сусідніх груп еквівалентних ядер
B₁ та B₂. ,

Для випадку ядер зі спіном ½

n_A = (N_B1 + 1)(N_B2 + 1) (1.21)

Якщо розглядати розщеплення на ядрах із спіном 1/2, то інтенсивності компонентів мультиплетів можна знайти за допомогою трикутника Паскаля:

У цьому трикутнику сума двох довільних елементів ряду дорівнює еле­менту, що розташований між ними в сусідньому нижньому ряду. Числа у кожному ряду трикутника Паскаля відповідають інтенсивностям компо­нентів мультиплету, що має стільки компонентів, скільки чисел міститься у даному ряду трикутника.

Для тих випадків, коли спіни ядер більші за 1/2, можна побудувати числові трикутники, подібні до трикутника Паскаля. Нижче наведені два такі трикутники для випадків I=1 та I=3/2. Тут, щоб дістати числа будь-якого нижнього ряду, додають вже не два, а три і відповідно чотири числа, що містяться у попередньому верхньому ряду (включаючи нулі справа і зліва від одиниць):

Кожний ряд трикутника дає змогу визначити інтенсивності компонентів мультиплету, утвореного внаслідок спін-спінової взаємодії ядра (або групи ядер) А з групою п ядер В, що мають спін I. Наприклад, сигнал ядер ¹³С моле­кули CD₄ складається з 7 компонентів, які мають відносні інтенсивності

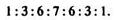
Описані правила ССВ називаються правилами розщеплення першого порядку. їх можна застосовувати у випадках, коли різниця хімічних зсувів взаємодіючих ядер перевищує їхню КССВ принаймні у шість разів.