Исследование функций
План полного исследования функции:
1. Элементарное исследование:
- найти область определения и область значений;
- выяснить общие свойства: четность (нечетность), периодичность;
- найти точки пересечения с осями координат;
- определить участки знакопостоянства.
2. Асимптоты:
- найти вертикальные асимптоты 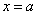 , если
, если 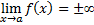
- найти наклонные асимптоты: y=kx+b, 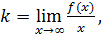
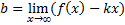
Если k=0, b - любое число, то y=b – горизонтальные асимптоты.
3. Исследование с помощью y’ - найти критические точки, те. точки в которых 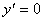 или не существует;
или не существует;
- определить интервалы возрастания, те. промежутки, на которых 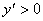 и убывания функции –
и убывания функции – 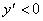 ;
;
- определить экстремумы: точки, при переходе через которые 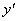 меняет знак с «+» на «–», являются точками максимума, с «–» на «+» – минимума.
меняет знак с «+» на «–», являются точками максимума, с «–» на «+» – минимума.
4. Исследование с помощью 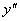 :
:
- найти точки, в которых 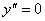 или не существует;
или не существует;
- найти участки выпуклости, т.е. промежутки, на которых 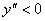 и вогнутости –
и вогнутости – 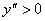 ;
;
- найти точки перегиба, т.е. точки при переходе через которые 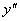 меняет знак.
меняет знак.
5. Построение графика функции.
Рекомендации по применению плана исследования функции:
1. Отдельные элементы исследования наносятся на график постепенно, по мере их нахождения.
2. Если появляются затруднения с построением графика функции, то находятся значения функции в некоторых дополнительных точках.
3. Целью исследования является описание характера поведения функции. Поэтому строится не точный график, а его приближение, на котором четко обозначены найденные элементы (экстремумы, точки перегиба, асимптоты и т.д.).
4. Строго придерживаться приведенного плана необязательно; важно не упустить характерные элементы поведения функции.
, то естьпри дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел 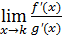 тоже должен существовать, в противном случае правило не применимо.***************************
тоже должен существовать, в противном случае правило не применимо.***************************
Примеры исследования функции:
20. 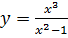
1) 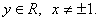
2) Функция нечетная:
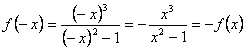 .
.
3) Асимптоты.
x-1, x+1 – вертикальные асимптоты, т.к. 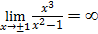
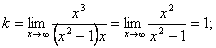
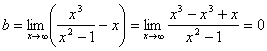
Наклонная асимптота y=x
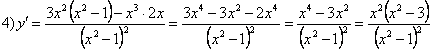
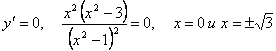
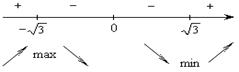
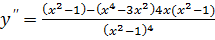 =
= 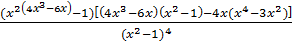
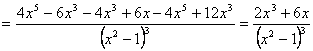
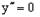
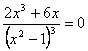
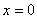 – точка перегиба.
– точка перегиба.
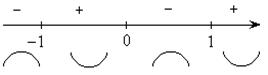
Схематичный график данной функции:
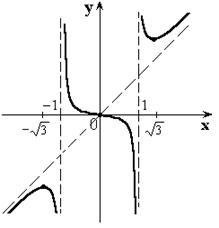
21. 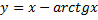
1) 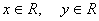
2) Функция нечетная:
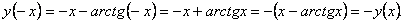
3) Асимптоты: Вертикальных асимптот нет.
Наклонные:

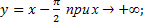
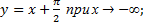 наклонные асимптоты
наклонные асимптоты
4) 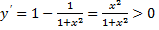 – функция возрастает.
– функция возрастает.
5) 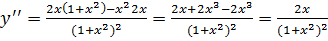
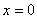 – точка перегиба.
– точка перегиба.
Схематичный график данной функции:
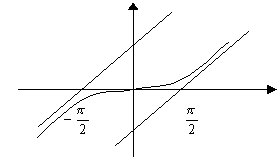
22. 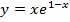
1) 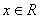
2) Функция общего вида
3) Асимптоты
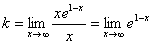
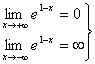 – наклонных асимптот нет
– наклонных асимптот нет
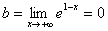
y=0 – горизонтальная асимптота при 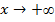
4) 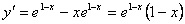
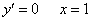
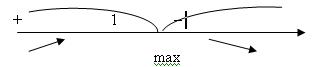
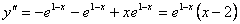
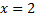 – точка перегиба
– точка перегиба
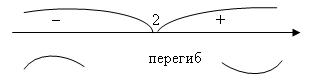
Схематичный график данной функции:
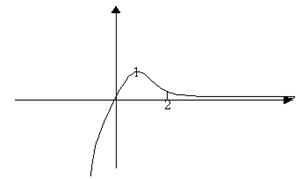
23. 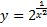
1) 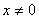
2) Асимптоты.
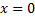 – вертикальная асимптота, т.к.
– вертикальная асимптота, т.к.
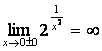
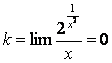 – наклонных асимптот нет
– наклонных асимптот нет
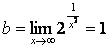 ,
, 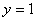 – горизонтальная асимптота
– горизонтальная асимптота
Схематичный график данной функции:
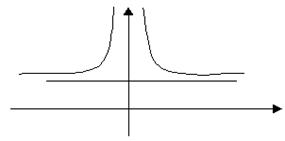
24. 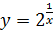
1) 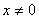
2) Асимптоты
x=0 – вертикальная асимптота при 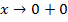 , т.к.
, т.к.
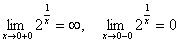
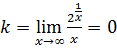 – наклонных асимптот нет
– наклонных асимптот нет
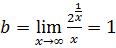 y=1 – горизонтальная асимптота
y=1 – горизонтальная асимптота
3) 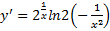 < 0 – функция убывает на каждом из промежутков.
< 0 – функция убывает на каждом из промежутков.
Схематичный график данной функции:
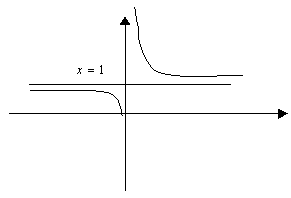
2.4.3 Наибольшее и наименьшее значение функции на отрезке
Чтобы найти наибольшее и наименьшее значение функции на отрезке можно воспользоваться схемой:
1. Найти производную функции 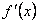 .
.
2. Найти критические точки функции, в которых 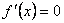 или не существует.
или не существует.
3. Найти значение функции в критических точках, принадлежащих заданному отрезку и на его концах и выбрать из них наибольшее 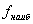 и наименьшее
и наименьшее 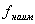 .
.
Пример. Найти наименьшее и наибольшее значение функции на данном отрезке.
25. 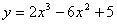 на промежутке
на промежутке 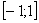
1) 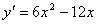
2) 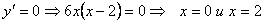 – критические точки
– критические точки
3) 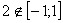 ,
,
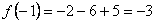 –
– 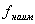
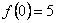 –
– 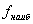
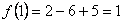
26. 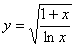 на промежутке
на промежутке 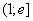 .
.
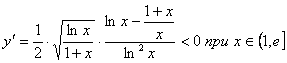
Прозbводная не существует при 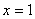 , но 1 не принадлежит данному промежутку. Функция
, но 1 не принадлежит данному промежутку. Функция 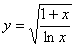 убывает на промежутке
убывает на промежутке 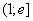 , значит, наибольшего значения нет, а наименьшее значение
, значит, наибольшего значения нет, а наименьшее значение 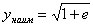 .
.
7 8 9 ... 13
Задание для самостоятельной работы
Исследовать функцию на экстремумы.
1. 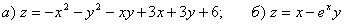 .
.
2. 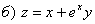 .
.
3. 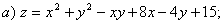
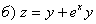 .
.
4. 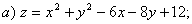
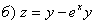 .
.
5. 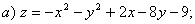
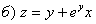 .
.
6. 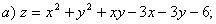
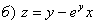 .
.
7. 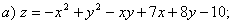
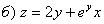 .
.
8. 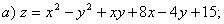
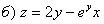 .
.
9. 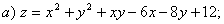
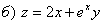 .
.
10. 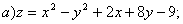
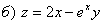 .
.
Задача 16. Найти наибольшее и наименьшее значение функции z=f(x,y) в данной замкнутой области.
1. Z= 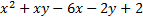 в прямоугольнике
в прямоугольнике 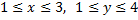
2. 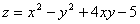 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 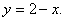
3. 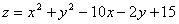 в прямоугольнике
в прямоугольнике
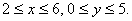
4. 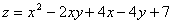 в области, ограниченной параболой
в области, ограниченной параболой
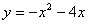 и осью абсцисс.
и осью абсцисс.
5. 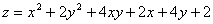 в квадрате
в квадрате 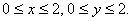
6. 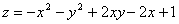 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 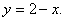
7. 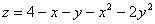 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 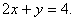
8. 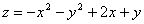 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 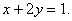
9. 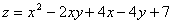 в области, ограниченной параболой
в области, ограниченной параболой
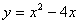 и осью абсцисс.
и осью абсцисс.
10. 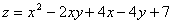 в области, ограниченной параболой
в области, ограниченной параболой
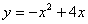 и осью абсцисс.
и осью абсцисс.
Пример. Найти предел 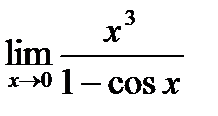 . (куда её?)
. (куда её?)
Так как 1 – cosx =  при х®0, то
при х®0, то 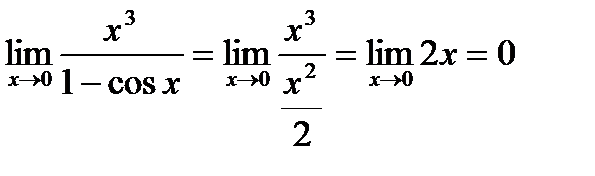 .
.
Дата добавления: 2015-08-11; просмотров: 1127;
