Критериальные уравнения конвективного теплообмена.

Можно, не решая уравнений, объединить физические величины в безразмерные комплексы и получить вид безразмерных (критериальных) уравнений с меньшим числом переменных. Решение этих уравнений позволяет находить искомые величины. Точные критериальные уравнения отыскиваются путем проведения соответствующих экспериментов. Примером безразмерного критерия подо­бия является критерий (число) Рейнольдса, хорошо известный из гидро­динамики:

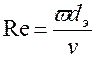, (2.4.1)

где 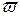– средняя скорость потока, м/сек;

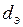– приведенный диаметр, м; 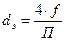(f – площадь поперечного сечения канала и 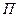– его смоченный периметр);

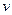– коэффициент кинематической вязкости, м²/сек.

Этот критерий определяет характер движения: для ламинарного движения 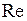< 2300, для турбулентного 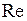имеет более высокое значение; так, для труб 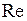> 1 • 104 (промежуточные значения относятся к неустойчивому движению).

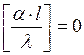, это означает, что и сам комплекс безразмерен.

Этот комплекс называют критерием (числом) Нуссельта и обоз­начают

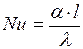(2.4.2)

Внешне критерий Нуссельта имеет вид, аналогичный критерию Био, разница заключается в том, что коэффициент теплопроводности в первом случае берется для газов, а во втором для обтекаемого тела.

Объединение характерных величин в безразмерные критерии позво­ляет определить количественные соотношения множества явлений.

Приведем еще пример получения безразмерного уравнения из размерного (недифференциального). Падение давления 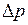в канале, имеющем диаметр d и длину 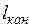, определяют но формуле Дарси:

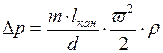н/м² (2.4.3)

здесь 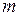– коэффициент трения, определяемый в свою очередь числом Re;

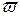– средняя скорость потока, м/сек.

Выразим потерю давления в долях от скоростного напора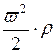

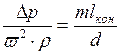. (2.4.4)

Величина слева представляет критерий Эйлера:

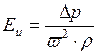(2.4.5)

Нам удалось определить критерий непосредственно из уравнения.

При приведении к безразмерному виду дифференциальных и других уравнений критерии точнее всего находят по методу масштабных преобразований.

В уравнении величина 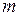является функцией критерия 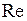и зависит также от шероховатости стен. Для данного материала канала уравнение перепишется в критериальном виде так:

.

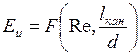Здесь 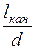– безразмерная длина канала,

Главнейшие безразмерные критерии тепловых и гидродинамических процессов

– Критерий Рейнольдса (критерий режима движения)

Характеризует соотношение сил инерции и определяет гидродинамический ражим движения.

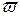– скорость, м/с;

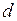– эквивалентный диаметр канала;

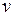– коэффициент кинематической вязкости, м²/сек.

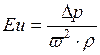– Критерий Эйлера (критерий падения давления)

Характеризует соотношение сил давления и инерции, а также безразмерную величину падения давления.

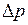– перепад давления, н/м²

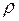– плотность жидкости, кг/м³

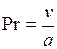– Критерий Прандтля (критерий физических свойств жидкости)

Характеризует физические свойства жидкости и способность распространения тепла в жидкости

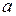– коэффициент температуропровожности, м²/сек

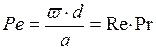– Критерий Пекле

Является мерой отношения молекулярного и конвективного переноса тепла в потоке.

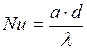– Критерий Нуссельта (критерий теплоотдачи)

Характеризует отношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока.

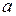– коэффициент конвективной теплоотдачи, вт/(м²∙град)

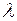– коэффициент теплопроводности жидкости (газа), вт/(м∙град)

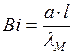– Критерий Био

Является мерой соотношения между внутренним и внешним термическим сопротивлениями.

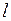– характерный размер тела, м;

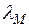– коэффициент теплопроводности твердого тела (материала), вт/(м∙град)

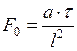– Критерий Фурье(безразмерное время)

Характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей, а также кинематическое подобие при свободном движении жидкости.

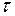– время, сек

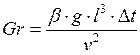– Критерий Грасгофа (критерий подъемной силы)

Используется при рассмотрении движения жидкости, в которой имеется взвесь твердых частиц или пузырьков. При 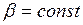идентичен критерию .

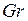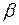– коэффициент объемного расширения, 1/град;

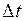– разности температур в двух точках системы потока и стенки, град

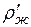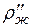Если и плотности жидкости в двух точках системы, то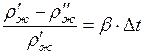

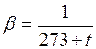
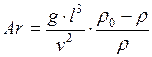– Критерий Архимеда

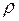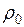и – плотности одной и другой фазы.