Теплопроводность плоской стенки

Для плоской стенки, или иначе для не­ограниченной пластины, когда 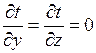, условие установивше­гося режима выражается уравнением:

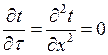. (2.2.1)

Решив это уравнение, получим 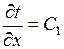и, следовательно,

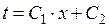. (2.2.2)

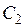где и – постоянные интегрирования.

Отсюда вытекает, что в плоской стенке без внутренних источников тепла температура распределяется по закону прямой линии (рис. 2.2.1).

Определив значения постоянных (положив один раз 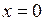, а другой раз 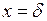) и подставив их в уравнение (38.2), найдем значение темпе­ратуры, в любой точке:

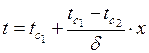(2.2.3)

Тепловой поток, проходящий через 1 м² стенки, можно выразить сле­дующим образом:

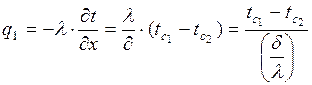(2.2.4)

Закон Фурье можно написать в форме, аналогичной закону Ома в элек­тротехнике, введя понятие о тепловом (термическом) сопротивлении:

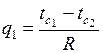вт/м²,

где 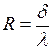– тепловое (термическое) сопротивление стенки, м²∙град/вт.

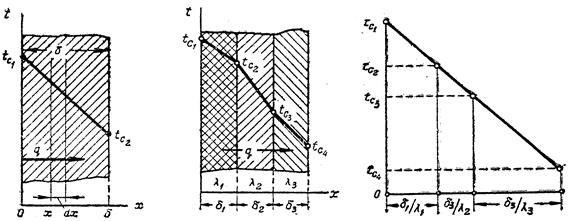
Рис. 2.2.1 Рис. 2.2.2 Рис. 2.2.3

Для сложной стенки, состоящей из 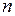слоев, тепловое сопротивление будет равно сумме сопротивлений отдельных слоев:

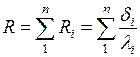(2.2.5)

И удельный тепловой поток может быть определен по формуле

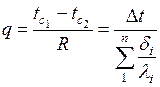(2.2.6)

Расределение температуры внутри стенки изображается ломаной прямой линией (рис. 2.2.2).

Если построить график изменения температуры как функцию термического сопротивления 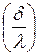, то он будет представлять прямую линию (рис.2.31.3). При помощи такого графика очень удобно определить температуры на границах слоев стенки.