Передача тепла теплопроводностью. Закон Фурье.

Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю.

Связь между количеством теплоты 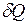, проходящим через элемен­тарную площадку 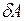, расположенную на изотермической поверх­ности, за промежуток времени 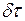, и градиентом температуры уста­навливается гипотезой Фурье, согласно которой

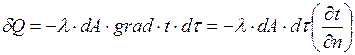. (2.1.1.1)

Минус в правой части показывает, что в направлении теплового потока температура убывает и grad t является величиной отрицатель­ной. Множитель пропорциональности 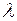называют теплопроводностью. Уравнение (2.1.1.1) носит название основного уравнения теплопровод­ности или закона Фурье. Справедливость гипотезы Фурье подтверж­дается опытами.

Отношение количества теплоты, проходящего через заданную по­верхность, ко времени называют тепловым потоком. Тепловой поток обозначают Ф и выражают в ваттах (Вт). Отношение теплового по­тока к площади поверхности называют поверхностной плотностью теплового потока (или вектором плотности теплового потока), обозначают и выражают в ваттах на квадратный метр (Вт/м²):

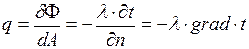, (2.1.1.2)

где 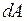– элементарная площадь;

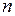– длина нормали к изотермиче­ской поверхности.

Вектор плотности теплового потока направлен по нормали к изо­термической поверхности в сторону убывания температуры. Векторы и 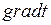лежат на одной прямой, но направлены в противополож­ные стороны.

Тепловой поток 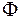, прошедший сквозь изотермическую поверх­ность площадью 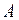, находят из выражения

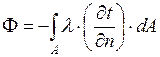. (2.1.1.3)

Количество теплоты, прошедшее через эту поверхность в течение времени ,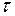

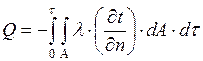(2.1.1.4)

Таким образом, для определения количества теплоты, проходя­щего через какую-либо произвольную поверхность твердого тела, не­обходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу ана­литической теории теплопроводности.