Изменении частоты вращения рабочего колеса

Наиболее экономичным способом регулирования работы насосного агрегата является изменение числа оборотов рабочего колеса. Зависимость подачи, напора и мощности центробежного насоса от частоты его вращения характеризуется следующими уравнениями:

; ; , (1.28)

где		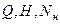- подача, напор и мощность при частоте вращения рабочего колеса ;
		- те же величины при другой частоте вращения рабочего колеса .

Приведенные три формулы выражают з а к о н п р о п о р ц и о - н а л ь н о с т и для центробежного насоса.

Высота всасывания насоса при работе его с частотой вращения определяется по уравнению:

, (1.29)

где		- допустимая вакуумметрическая высота всасывания при частоте вращения n;
		- то же, при частоте вращения .

Закон пропорциональности позволяет по одной характеристике 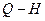построить ряд характеристик насоса в широком диапазоне частоты вращения.

Решая совместно первые две формулы закона пропорциональности, получим уравнение параболы подобных режимов:

, (1.30)

где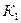

- коэффициент, характеризующий кривую пропорциональности.

Для одной параболы подобных режимов коэффициент пропорцио-нальности постоянен.

Имея характеристику насоса 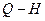для частоты вращения и поль-зуясь формулами пропорциональности и , можно построить новую характеристику насоса для другой частоты .

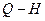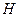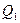Для этого надо задаться на известной кривой какой-либо точкой 1 с параметрами и при частоте вращения (рис. 1.11) и, поставив их в уравнения и , найти и 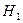для точки 1^' с заданной частотой вращения . Так же находят параметры точек 2', 3' и т.д. Соединив эти точки, получим кривую , новую характеристику насоса для частоты вращения .

При построении кривой КПД пользуются тем, что КПД насоса при изменении частоты вращения рабочего колеса насоса в довольно широких диапазонах остается практически постоянным. Поэтому КПД, соответствующий точкам 1, 2, 3, 4 и т.д. на кривой 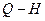, переносят без изменения соответственно точкам 1', 2', 3', 4' и т.д.

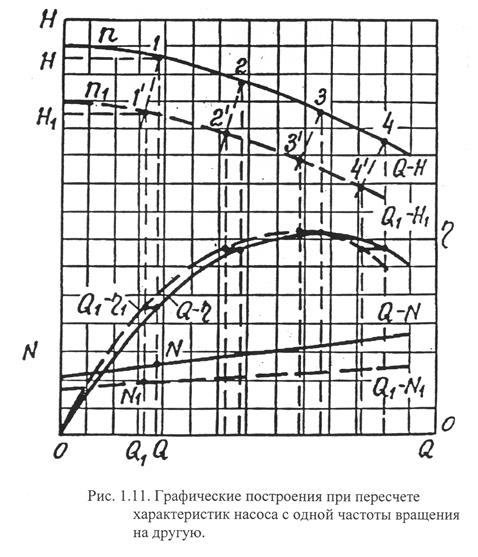
Кривую мощности 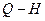пересчитывают по третьей формуле закона пропорциональности .