Проверка прочности круглых стержней при кручении с изгибом
Будем рассматривать только круглые стержни.
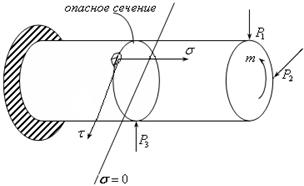
рис.19.8
Пусть стоит задача: проверки прочности в опасном сечении. Исследуем малый элемент в опасном сечении (см.рис.19.8)

рис.19.9
Особенность ситуации в том, что на элемент действуют два вида напряжений одновременно, поэтому условие прочности вида 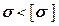 ,
, 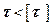 , не обеспечивают прочность, поскольку они справедливы только при простом растяжении и при простом сдвиге. Так как
, не обеспечивают прочность, поскольку они справедливы только при простом растяжении и при простом сдвиге. Так как 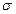 и
и 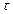 действуют одновременно, то в зависимости от материала, нужно применять различные теории прочности.
действуют одновременно, то в зависимости от материала, нужно применять различные теории прочности.
Для стали, в запас прочности, можно использовать III теорию:
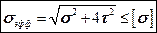 (19.3)
(19.3)
Здесь 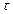 вычисляется как обычно:
вычисляется как обычно: 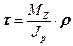
Для полого вала 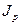 имеет вид:
имеет вид:
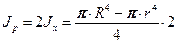 (19.4)
(19.4)
Для отыскания 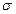 для круглых стержней не обязательно находить опасную точку. Действительно, если найдена нейтральная линия, то мы можем принять её за ось
для круглых стержней не обязательно находить опасную точку. Действительно, если найдена нейтральная линия, то мы можем принять её за ось 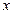 .
.

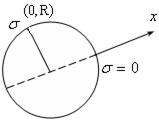
рис.19.10
В этом случае опасной будет точка с координатами х = 0, у = R (рис.19.10). Изгибающий момент тогда вычисляется как геометрическая сумма 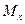 и
и 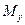 :
:
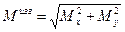 (19.5)
(19.5)
Поэтому по формуле Навье найдем:
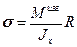 ,
, 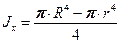 .
.
Если кроме кручения и изгиба имеется растяжение, то максимальное значение напряжения 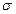 вычисляется по формуле:
вычисляется по формуле:
 (19.6)
(19.6)
Дата добавления: 2015-08-11; просмотров: 800;
